Устойчивость линейных непрерывных систем

Физически устойчивость означает, что при ограниченном входном воздействии выходной сигнал также является ограниченным и процессы в системе стремятся к определенному значению при любых начальных условиях. Качественный вид переходных характеристик устойчивой и неустойчивой систем изображен на рис. 4.1. Очевидно, что для переходной характеристики устойчивой системы справедливо условие. Отметим, что… Читать ещё >
Устойчивость линейных непрерывных систем (реферат, курсовая, диплом, контрольная)
В результате изучения материала данной главы студент должен: знать
- • методы оценки устойчивости линейных систем автоматического управления;
- • способы определения областей и запасов устойчивости систем управления; уметь
- • применять адекватные критерии устойчивости для анализа свойств систем автоматики;
- • оценивать влияние параметров динамической системы на ее устойчивость; владеть
- • различными методами анализа устойчивости линейных систем автоматики.
Введение
В этой главе мы начинаем исследование свойств процессов, происходящих в системах автоматики. Важнейшим из них является устойчивость — основное качественное свойство системы автоматического управления, без которого она неработоспособна.
Физически устойчивость означает, что при ограниченном входном воздействии выходной сигнал также является ограниченным и процессы в системе стремятся к определенному значению при любых начальных условиях.
Отметим, что в случае линейных систем устойчивость определяется только ее структурой и параметрами и не зависит от величины внешних воздействий и начальных условий.
Качественный вид переходных характеристик устойчивой и неустойчивой систем изображен на рис. 4.1. Очевидно, что для переходной характеристики устойчивой системы справедливо условие.
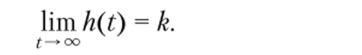
Об устойчивости можно судить также по импульсным переходным функциям (рис. 4.2), которые в случае устойчивой системы удовлетворяют условию 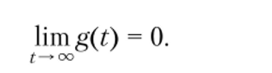
Рассмотрим, как можно оценить это свойство для систем, поведение которых описывают уравнения.

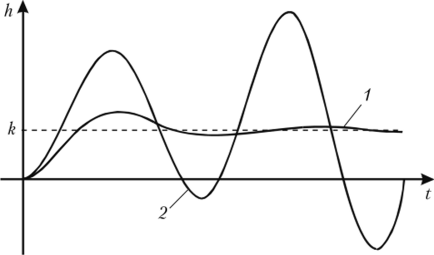
Рис. 4.1. Переходные характеристики системы:
1 — сходящийся процесс, система устойчива; 2 — расходящийся процесс, система неустойчива.
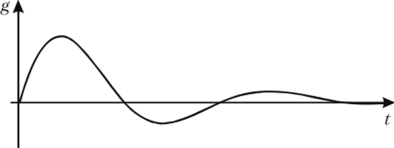
Рис. 4.2. Импульсная переходная функция устойчивой системы.
Переходные процессы определим как решение векторно-матричного уравнения состояния следующим образом:
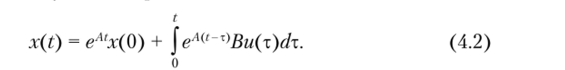
Здесь первое слагаемое соответствует свободной составляющей движения (из произвольных начальных условий), второе — вынужденной (движение под действием управления).
Одним из основных режимов работы системы управления является равновесный (статический) режим, при котором переменные состояния с течением времени не меняются, а все производные координат состояния равны нулю.
Покажем, что процесс движения к равновесию можно считать свободным, т. е. он соответствует первому слагаемому в выражении (4.2).
Предварительно запишем уравнение статики, полагая в системе (4.1)х= О, и = const:

откуда при det А * 0 определим равновесное значение переменных состояния.

Введем новые координаты, равные отклонениям от точки равновесия:

и запишем уравнение в отклонениях: так как х° = 0.

После подстановки в уравнение (4.6) вместо х его значения из системы (4.1) с учетом соотношения (4.5) получим.

Уравнение в отклонениях имеет вид.

Как видим, уравнение (4.7) не содержит и, и переходный процесс по Д порождается только ненулевыми начальными условиями согласно уравнению.

Линейная система называется устойчивой, если для ее процессов выполняется свойство.

Условие (4.9) представляет собой предел выражения (4.8), которое соответствует первой составляющей решения (4.2). Таким образом, устойчивость линейной системы (4.1) определяется только свойствами автономной системы и не зависит от внешних воздействий. Это означает, что для анализа устойчивости можно не переходить к уравнениям в отклонениях от состояния равновесия, а исследовать свойства матрицы А.