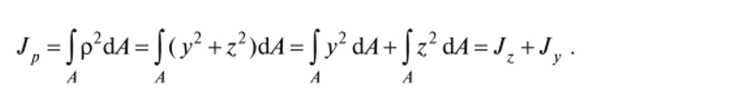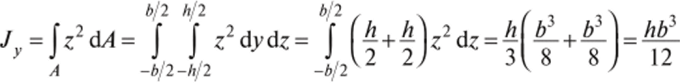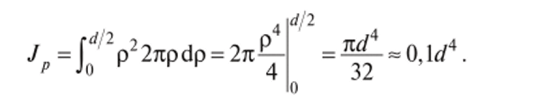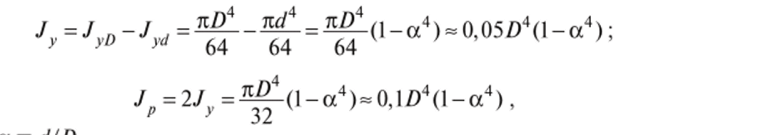Моменты инерции сечений

Моментами инерции сечений называются интегралы следующего вида.

Свойства моментов инерции.

Размерность моментов инерции — [длина⁴1, обычно [м⁴] или [см⁴|. Осевые и полярный моменты инерции всегда положительные. Центробежный момент инерции может быть положительным, отрицательным или равным нулю. Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции сечения. Оси симметрии всегда главные. Если из двух осей хотя бы одна является осью симметрии, то обе оси главные.

Момент инерции составного сечения равен сумме моментов инерции элементов этого сечения. Полярный момент инерции равен сумме осевых моментов инерции. Докажем последнее свойство. В сечении площадью А для элементарной площадки dA радиус-вектор р и Л П Л.

координаты ywz (рис. 2.4) связаны. По теореме Пифагора р = у +z. Тогда.

Моменты инерции простейших фигур.

Получим формулы для моментов инерции относительно собственных центральных осей простейших фигур: прямоугольника, круга, треугольника.

Прямоугольник. Пусть ywz — оси симметрии прямоугольного сечения. Выберем в сечении (рис. 2.5) элементарную площадку с14 с координатами ywz. Площадь dA = dydz. Осевой момент инерции относительно оси у

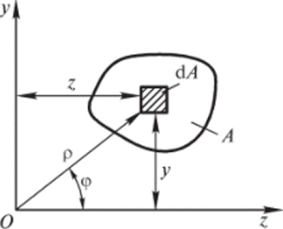
Рис. 2.4. Связь полярных и декартовых координат элементарной площадки.

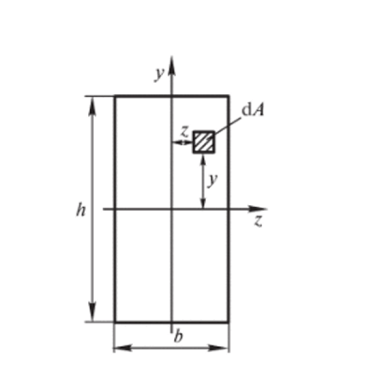
Рис. 2.5. К определению моментов инерции прямоугольного сечения.

Аналогично получаем момент инерции относительно оси Z'. J_z — bh³/12. Поскольку >> и z — оси симметрии, то центробежный момент Лу = 0.

Круг и кольцо. Для круга диаметром d вычисления упрощаются, если использовать круговую симметрию. Возьмем в качестве элементарной площадки бесконечно тонкое кольцо радиусом р и толщиной dp (рис. 2.6). Его площадь dA = 2npdp. Тогда полярный момент инерции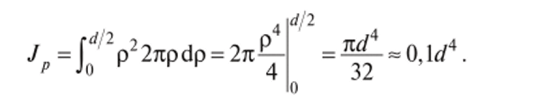

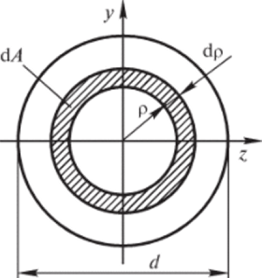
Рис. 2.6. К определению моментов инерции круга.

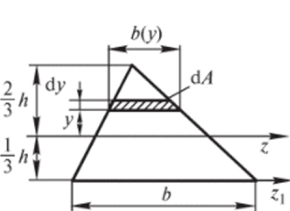
Рис. 2.7. К определению момента инерции треугольника.

Ввиду круговой симметрии осевые моменты инерции относительно любой центральной оси одинаковы: J_y = J_z — J_p/2 = л</<sup>4/64 * 0,05*/⁴.

где, а = а{ и.

Момент инерции кольца находим как разность моментов инерции двух кругов:

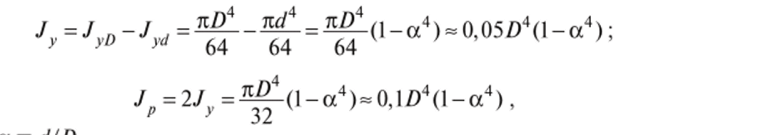
Момент инерции треугольника. Найдем момент инерции треугольника относительно центральной оси г₀, параллельной основанию (рис. 2.7). Выделим элементарную площадку dA параллельную основанию: d А = b (y)dy.

Из подобия треугольников 2(h—y)/h = b (y)/b. Откуда Момент инерции У. вычислим с помощью Mathcad символьным путем. В формуле для У. параметры можно не писать. Результат будет гот же, но выражение окрасится в красный цвет. Численное вычисление — запрещено, символьное — возможно.