Способы оценки градиента

Задача непрерывной оценки градиента представляет собой самостоятельную и очень непростую техническую проблему. К настоящему времени разработаны различные способы оценки как величины, так и знака градиента. Остановимся на некоторых из них.

Способ деления производных

Рассмотрим суть данного способа на примере одноканальных объектов, статическая экстремальная характеристика которых имеет вид.

Определим полную производную выходной переменной по времени:

Второе слагаемое в выражении (11.9) обусловлено наличием дрейфа. При медленном дрейфе экстремальной характеристики им можно прене- «5Y

бречь, так как —-*• 0. В этом случае из выражения (11.9) можно опреде;

ду

лить величину градиента как отношение двух полных производных, но времени:

Структурная схема устройства, реализующего оценку градиента по методу деления производных, представлена на рис. 11.6.

Поскольку операция дифференцирования на практике очень критична к помехам, для оценки производных следует использовать дифференцирующие фильтры ДФ (на рис. 11.6 они показаны пунктиром).

Достоинством данного способа является простота технической реализации.

Недостатками являются техническая сложность оценки градиента при малых значениях у (как следует из выражения (11.10)) и слабая помехозащищенность. Для уменьшения влияния помехи рекомендуется использовать дифференцирующие фильтры выше первого порядка (см. гл. 10).

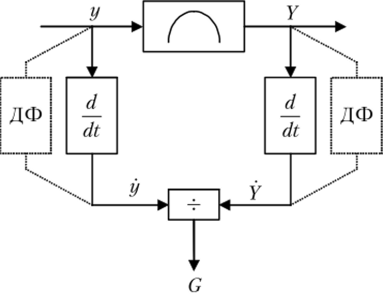
Рис. 11.6. Структурная схема устройства оценки градиента методом деления производных.