Основные понятия теории подобия

Теория подобия рассматривает подобие явлений и присущих им свойств в геометрически подобных аппаратах. При геометрическом подобии фигур отношение всех сходных размеров этих фигур должно быть постоянно [6, 13, 17].

В двух кинематических системах должно быть кинематическое подобие, если их сходственные частицы передвигаются по геометрически подобным путям в промежутки времени, отличающиеся постоянным множителем. В этом случае можно говорить о подобии движения, например, двух потоков жидкости. При динамическом подобии многоугольники сил для пары сходственных частиц в пространстве и во времени должны быть подобны, т. е. различаться лишь масштабом.

Понятие подобия можно также распространить на тепловые и физико-химические процессы.

Для использования понятий о подобии необходимо найти условия подобия рассматриваемых явлений. При этом возникают следующие вопросы:

• — возможно ли опытные данные, полученные путем измерения в аппарате лабораторных размеров (на физической модели), перенести на другой аппарат (промышленный).
• — каковы условия такого переноса или пересчета.
• — как следует опытные данные, полученные на физической модели, использовать для промышленного аппарата.

Перенос опытных данных с физической модели возможен в случаях, когда имеется подобие обоих процессов. Это подобие не должно ограничиваться только геометрическими параметрами; все другие величины, которые влияют, например, на массоили теплопередачу, должны в физической модели и в промышленном аппарате находиться в определенных соотношениях.

Отыскание условий подобия производится следующим образом. Сравниваются такие два случая, при которых подобны потоки для всех величин, встречающихся в уравнениях: неразрывности, Навье-Стокса для несжимаемой и сжимаемой жидкости, теплового баланса.

Таковыми величинами являются координаты промышленного аппарата х, у, z, которые относительно модели с координатами х у z' могут быть равномерно увеличены.

Следовательно, сопоставляются потоки, которые проходят через геометрически подобные тела или вокруг них. Тогда все отрезки промышленного аппарата //, /?, /3,… будут увеличены в определенной пропорции по отношению к физической модели с отрезками //', // //,…

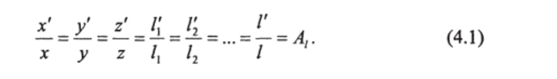
При строгом соблюдении геометрических условий подобия неровности (шероховатости) поверхностей по форме и величине в промышленном аппарате и в физической модели должны быть подобны. Однако на практике это условие вряд ли может быть выполнено.

Поля скоростей в промышленном аппарате со'и физической модели со должны быть подобны, т. е.

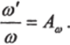
Кроме того, направление соответствующих скоростей (<�у, й/) должно быть одно и то же. Таким образом, подобие между ламинарным и турбулентным потоками невозможно, так как распределение скоростей в обоих потоках принципиально различно. Можно сравнивать ламинарные потоки только между собой, как и турбулентные потоки.

Следующей важной величиной является температурный градиент дТ дТ дТ _п

—,—. Распределение градиентов должно быть подобным, т. е. дх ду oz

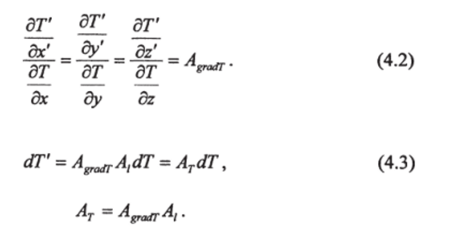
Из (4.1) имеем:

Интегрируя уравнение (4.3) получим:

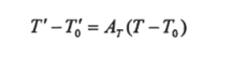
или.

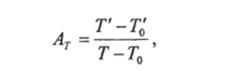
где Tq и Т₀ — произвольные постоянные интегрирования для произвольно выбранных точек x'₀, y'₀, z'₀ и x₀, y₀, z₀.

В физической модели и промышленном аппарате температуры Г₀' и Т₀ могут быть выбраны, например, у входа в трубопровод или на большом расстоянии от стенки в зависимости от целесообразности. В уравнение подобия температурных полей входят не температуры, а их разности по отношению к температуре произвольно выбранной точки.

Из уравнений (4.1) — (4.3) следует:

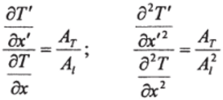
Во многих случаях имеет значение соблюдение подобия градиентов концентраций в материальных потоках, проходящих через аппараты. Условия подобия концентрационных и температурных градиентов аналогичны.

Статическое давление входит в дифференциальные уравнения в виде др

градиентов — и т. д.; по аналогии с температурным полем можем записать дх

условие подобия для поля давления:

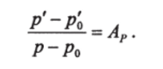
Подобие полей физических свойств среды обуславливает следующие постоянные соотношения для всех соответственных точек в промышленном аппарате и физической модели:

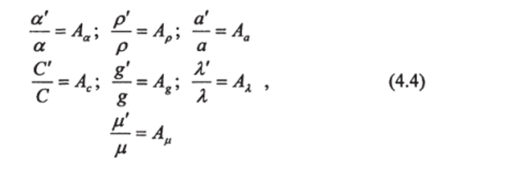
где р-плотность; цвязкость; X- теплопроводность; акоэффициент теплоотдачи; g- ускорение свободного падения; а — коэффициент температуропроводности; С — теплоемкость.

Следует отметить, что при выполнении условий подобия не все масштабные множители А, могут быть произвольно выбраны.

НаЦример, если увеличить скорость движения жидкости в трубо;

(й>

проводе вдвое, т. е. А_а = — = 2, то перепад давления р- р₀, вследствие.

со

трения, возрастает, как известно, пропорционально квадрату скорости, т. е.

t_ г

А_р =— = 4. Масштабный множитель А_р в данном случае определя;

Р-Ро

ется через подобие скоростных полей.

Пользуясь этими соображениями, приходам к заключению, что число независимых масштабных множителей Л/ по сравнению с приведенными в уравнениях (4.1) — (4.4) может существенно сократиться в силу дополнительных условий.

Для того чтобы определить физический смысл критерия (числа) подобия, определяемый экспериментальным путем, необходимо составить математическое описание изучаемого процесса (гидродинамики, теплообмена, диффузии и т. д.).