Вынужденные колебания системы с п степенями свободы

Упругая система подвержена действию силы, изменяющейся во времени. Надо определить перемещения системы во времени, вызванные действием заданной силы. Для этого надо решить уравнение движения системы (24.1). Решать это уравнение целесообразно методом прямого интегрирования с помощью пошаговой численной процедуры, использующей метод конечных разностей. Никаких предварительных преобразований уравнения движения не производится.

Заданный промежуток времени, в котором надо определить узловые перемещения Д (/), разбивают на отдельные временные точки tj = Д//, где At — временной шаг интегрирования. Скорость V. = Д' и Подставив выражения (24.12) в уравнение движения (24.3), можно найти узловые перемещения {А,} в момент времени На каждом шаге интегрирования, по существу, решается статическая задача. Равновесие с учетом сил демпфирования и инерции рассматривается в выбранных точках временного интервала.

Методы прямого интегрирования различаются способами интерполяции или экстраполяции на каждом малом временном интервале. В рассмотренных в электронной книге примерах к методу конечных элементов использован метод Ньюмарка, называемый также методом обобщенного ускорения. В этом методе используются следующие конечно-разностные соотношения:

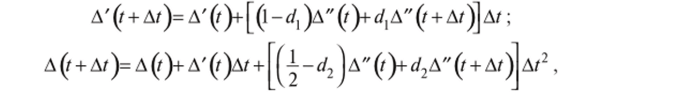
где d_]ud₂ — параметры интегрирования. При d_x = 0,5 и d₂ = 0,25 приведенные соотношения будут отвечать предположению о постоянном характере ускорения на временном интервале (/; f+ At), при dj = 0,5 и d₂ =1/6 — о линейном изменении ускорения, что аналогично методу Вилсона. При d₂ = 0 получим центрально-разностную схему вычислений, соответствующую двойной пульсации ускорения в начале и в конце каждого временного интервала. Таким образом, d₂ определяет закон изменения ускорения в пределах шага счета.

Параметр d_] характеризует схемное (численное) демпфирование: при 0 < </, < 0,5 — отрицательное, при d_x > 0,5 — положительное, при d_x = 0 схемное затухание отсутствует. При решении конечномерных задач большой размерности рекомендуется принимать d_x >0,5 и d₂ >0,25.

Уравнение движения (24.3) преобразуется к виду.

ускорение а. = А" в момент времени 1, можно определить по конечно-разностным формулам:

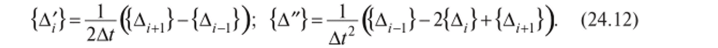
Здесь [к] и {Q} — так называемые эффективные матрица жесткости и вектор нагрузок, содержащие матрицы [Л/_]_, [Я], [А'] и шаг интегрирования А/. Выражения для определения [А'] и {0}приведены в Mathcad-программах примеров, приведенных в электронной книге. Из уравнения (24.13) определяют вектор узловых перемещений {А (г)} в момент времени /. Приведенный алгоритм реализует неявную двухслойную схему интегрирования.

Для достижения приемлемой точности расчета шаг интегрирования At должен быть меньше наименьшего периода собственных колебаний, существенно влияющего на поведение системы. Однако при малом шаге интегрирования растет погрешность расчетов. Анализируя результаты расчета и варьируя параметры интегрирования, можно добиться соответствия результатов здравому смыслу или результатам эксперимента.