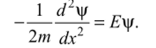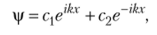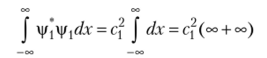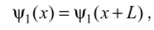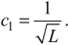Решения уравнения шрёдингера для простейших задач

Рассмотрим простейшие примеры решения уравнения Шрёдингера для стационарных состояний, имеющие прямое отношение к химическим задачам. Существенное влияние на характер получаемых решений уравнения оказывают граничные условия задач. В частности, они определяют, будет ли спектр собственных значений гамильтониана дискретным или непрерывным.

Одномерная модель свободной частицы

Свободной называется частица, потенциальная энергия которой в любой точке пространства одинакова. Свободные электроны, например, образуются в процессах ионизации молекул. Они участвуют на первом этапе в реакциях захвата электронов.

Для удобства обычно считают, что U = 0. В этом случае одномерное уравнение Шрёдингера для стационарного состояния частицы, движущейся вдоль оси х, имеет вид.

Введя обозначение k² = 2тЕ, получаем.

Общее решение такого уравнения следующее:

где Cj и с₂ — произвольные постоянные.

Общее решение есть линейная комбинация двух волн де Бройля, соответствующих импульсам р_х и -р_х.

Ограничимся рассмотрением одной волны, бегущей в положительном направлении оси х:

Условие нормировки данной функции стандартным образом получить не удается, так как интеграл.

расходится. Чтобы осуществить нормирование функции, можно в качестве ограничения на свойства функции наложить условие ее периодичности:

где L — длина периодичности.

В принципе данное ограничение не является существенным, так значение L может быть выбрано сколь угодно большим. Теперь благодаря периодичности функции на отрезке L условие ее нормировки приобретает вид.

Поэтому.

Из условия периодичности находим где п = 0, ±1, ±2,…;

Теперь благодаря использованной подстановке k¹ = 2тЕ выражение для энергии частицы и ее волновая функция приобретают более конкретный вид.

Условие периодичности делает энергетический спектр частицы дискретным, однако при /,—>о спектр получается непрерывным.