Б. Вращение системы, как целого

Проблема выделения переменных, отвечающих вращению свободной системы как целого, гораздо сложнее проблемы выделения переменных центра масс. В то же время выделять их надо, ибо в противном случае распределение плотности вероятности каждой частицы должно быть по физическим соображениям сферически симметрично, каждая молекула должна представлять собой шарик с каким-то распределением радиальной плотности для каждой частицы, в эту молекулу входящей'.

В классической механике вращение системы определяется ее угловой скоростью в данный момент времени, если используется лагранжев формализм, и моментом импульса (т.е. моментом количества движения, угловым моментом), если используется гамильтонов формализм, на базе которого строится и квантовая механика. Если угловой момент равен нулю, то вращение системы отсутствует. Казалось бы, наиболее естественный путь отделения вращательных переменных заключается в том, чтобы перейти от исходной инерциальной лабораторной системы координат к новой системе, вращающейся относительно исходной, а потому — неинерциальной, в которой угловой момент равнялся бы нулю. Однако сделать это не так-то просто. Действительно, для перехода от одной системы координат к другой у нас должны быть уравнения, связывающие переменные одной системы с переменными другой, например уравнения вида q_t = <7,(г, г₂,…, Гд,), /= 1, 2,…, 3N. Если среди переменных Г|, r₂,…, r_N есть зависимые, a q_t- независимые переменные, то / может быть и меньше 3jY, причем тогда должны существовать уравнения связи вида^(г, г₂,…, Гд,) = 0, к — 1,2,…,/, которые и позволяют выделить независимые переменные. Как уже сказано, хотелось бы ввести такую систему координат, в которой выполнялись бы условия L_x = L_y = L_z = 0, т. е., например:

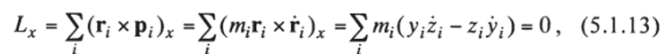
где г, — скорость движения /-й частицы, а р, — ее импульс; скобки (axb)_x означают, что взята лг-компонента векторного произведения. Эти условия, связывающие вращающуюся систему координат с системой материальных точек (молекулой) отличаются от условий f_k = 0 тем, что они содержат скорости г,. Перейти от них к условиям вида f_k(г, г₂, …, Гдг) = 0 в общем случае нельзя, ибо дифференциальные уравнения первого порядка вида (13) в общем случае не являются интегрируемыми. Следовательно, условия равенства нулю компонент момента импульса не дают возможности найти такие уравнения, которые определяли бы угловые.

'Нет оснований для какого-либо выделенного направления или выделенной конфигурации частиц, отличающейся от другой конфигурации лишь поворотом вокруг произвольной оси, проходящей через центр масс, на произвольный угол.

переменные, задающие положение подвижной системы координат относительно неподвижной, через все остальные координаты частиц молекулярной системы.

Введем теперь несколько формул, поясняющих сказанное выше. Положение осей подвижной системы координат Oxyz относительно осей неподвижной, лабораторной системы OXYZ может быть определено тремя углами Эйлера ср, О и х (рис. 5.1.2), которые задают три последовательных поворота от одной системы к другой (начала обеих систем координат совпадают). Первый поворот совершается вокруг оси OZ в положительном направлении на угол ф. Ось OZ при этом не меняется, равно как не меняется и проекция Z произвольного радиуса-вектора R на эту ось. Компоненты.

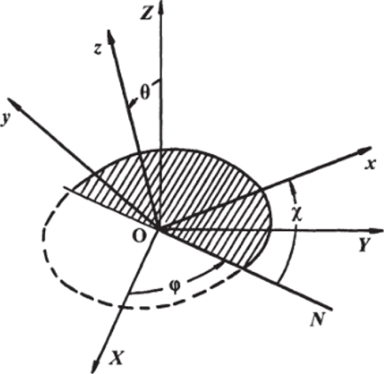
Рис. 5.1.2. Углы Эйлера, определяющие положение подвижной системы координат Oxyz относительно неподвижной (лабораторной) системы OXYZ: <�р — угол прецессии, О — угол нутации ихугол собственного вращения.

вектора R в новой системе Ox’y’z' определятся следующим преобразованием (по существу, преобразуются лишь Л" и К в.

х' = X соэф + Y sin.

— X sinq> + Y соэф):

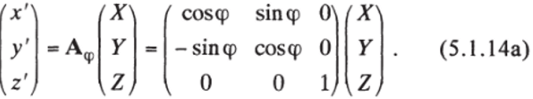
Второй поворот совершается вокруг оси Ох' на угол Ф, так чтобы новая ось Oz" совпала с осью Oz подвижной системы координат.

(это совпадение определяет и величину угла <�р, поскольку линия Ог' должна лежать в плоскости x’OZ):

Наконец, третий поворот совершается вокруг оси Oz" на угол /, так чтобы ось Ох" совпала с осью Ох, а Оу"  — с осью Оу:

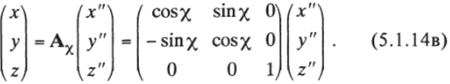
Результирующий поворот определяется последовательностью трех указанных поворотов, т. е. матрицей, А = А_х-А₉ А_ф. Коль скоро каждая из матриц-сомножителей ортогональна (в чем нетрудно убедиться прямой проверкой), то ортогональной будет и матрица А. Итак, имеем:

где г — вектор-столбец из компонент вектора в подвижной системе, a R — вектор-столбец из компонент того же вектора в неподвижной системе координат.

Скорости изменения г и R с течением времени связаны следующим соотношением, получающимся при дифференцировании (15) по времени:

Здесь А*- матрица, получающаяся из А* взятием производной по времени от каждого ее элемента, причем АА^ = 1. Что касается матрицы АА*, то ее структура очень проста:

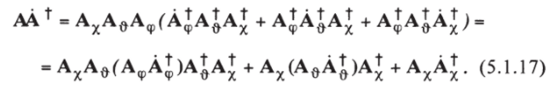
Поскольку далее.

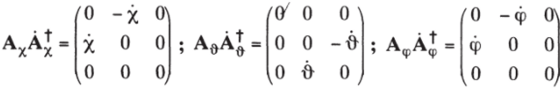
и X > # ^и Ф ^- величины векторов угловой скорости ш, направленных по осям Oz, Ох' (называемой линией узлов) и OZ соответственно. Поэтому.

где <�о_г — угловая скорость вращения вокруг оси Oz, направленная по этой оси, так что ее проекция (со₂)₂на эту ось совпадает с длиной вектора <�о₂; далее.

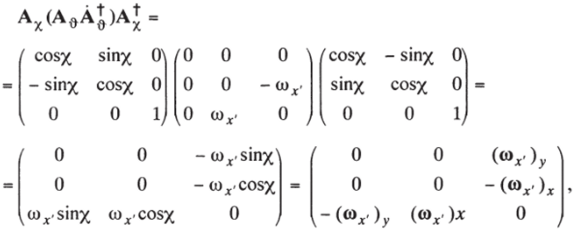
где ш₂. — длина вектора угловой скорости при поворотах вокруг линии узлов, а (со₂.)₂ и (со_г)_х — проекции этого вектора на оси подвижной системы координат. Аналогично записываются элементы и оставшейся в правой части (16) матрицы А_хА_в(А_фА_ф)А^А_х через проекции вектора z, отвечающего поворотам вокруг оси ОZ неподвижной системы. Коль скоро полная угловая скорость со системы есть векторная сумма указанных трех угловых скоростей: со = со₂ + + to_z, то окончательно найдем:

Следовательно,.

т.е. скорость R в лабораторной системе координат, как показывают (16) и полученное равенство, есть записанная в этой системе сумма собственной скорости г и скорости со х г, обусловленной вращением подвижной системы координат:

Для частицы с массой т момент импульса с использованием (15) можно теперь записать так:

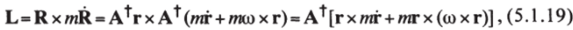
где переход к последнему равенству основан на том, что слева в нем стоит векторное произведение двух векторов в лабораторной системе, а справа записано сначала это же векторное произведение в подвижной системе, а потом совершен обратный переход к лабораторной системе. Вектор 1 = г хтг есть момент импульса в подвижной системе (который, как очень хотелось бы, должен быть по возможности близким нулю). Двойное же векторное произведение можно переписать, применяя известную формулу векторного исчисления:

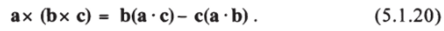
Тогда получим.

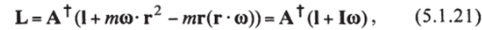
причем I — симметричная матрица, элементами которой служат моменты инерции (на диагонали) и так называемые произведения инерции (на недиагональных местах):

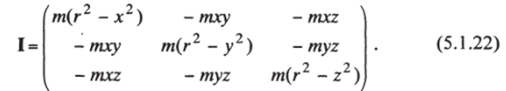
Для системы материальных точек матрица I будет суммой матриц (22), относящихся к отдельным точкам. Эту матрицу часто называют матрицей тензора инерции. Используя соотношение (21), можем найти выражение для со и подставить его в (18):

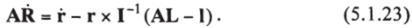
Таким образом, скорость R в лабораторной системе координат выражена через скорость в подвижной системе, через момент импульса L в лабораторной системе и через момент импульса I в подвижной системе. Подставим выражение (23) для скорости R_; каждой материальной точки в функцию Лагранжа и попробуем перейти далее к функции Гамильтона (с тем, чтобы записать далее оператор Гамильтона). При этом переход к импульсам потребует использования независимых координат и построения канонически сопряженных им импульсов.

Будем использовать в качестве таких независимых координат относительные координаты частиц q_t (/ = 1, 2,…, и, где п для свободной системы N материальных точек равно в общем случае 37V-6), углы Эйлера, связывающие подвижную систему с лабораторной, и координаты центра масс. В качестве 6 условий связи подвижной системы с молекулой примем следующие:

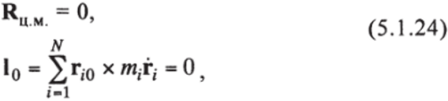
где r_/0 — некоторая фиксированная конфигурация частиц (всех или только лишь части) рассматриваемой молекулярной системы. Второе из этих векторных условий допускает переход к конечным уравнениям, не содержащим скоростей:

где с — постоянный вектор.

Условия (24) для молекул обычно записывают так, что они относятся только к ядерной подсистеме. В этом случае они носят название условий Эккарта. Такая запись связана, конечно, с опреде-ленными приближениями, обсуждать которые детальнее не будем. Последующий переход к функции, а затем и оператору Гамильтона приводит после ряда довольно громоздких преобразований к га-мильтониану вида:

где L_a — компоненты момента импульса всей молекулярной системы (L_x, L_y и L_z при, а = 1, 2 и 3 соответственно), р_к — операторы импульсов (-itid/dq_k), канонически сопряженных относительным обобщенным координатам q_k; (1^-1)_ар ~ элементы матрицы, обратной матрице (22), t_kl — элементы матрицы кинетической энергии относительного движения частиц, V (q) — потенциал взаимодействия частиц друг с другом, и, наконец, С_ак-

элементы матрицы размера 3хп, где п — число независимых относительных переменных q_k. Все величины (1″^!)_ар, t_kJ и С_ак суть функции этих относительных переменных.

Если записать операторы L_a в виде вектора-столбца L, операторы р_к — в виде вектора-столбца Р (с п компонентами), а также ввести соответствующие матрицы I^-1, Т и С, то матричное представление гамильтониана (25) будет выглядеть следующим образом:

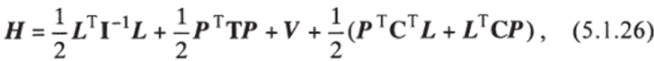
В выражении (25) или (26) первый член соответствует вращению системы как целого, хотя он через посредство элементов матрицы I^-1 зависит и от относительных координат. В этом члене в действительности должен был бы стоять вектор L — /, где / - оператор, соответствующий угловому моменту I в подвижной системе; однако этот оператор в предположении его малости мы пока опускаем. Если второе условие Эккарта записывается только лишь для ядерной подсистемы, то / будет включать момент импульса электронов и так называемый колебательный момент импульса ядер, который за счет того, что момент импульса ядер в существенной степени оказывается исключенным этим вторым условием, является малым, и им действительно обычно пренебрегают. Следующие два члена в правой части (25) или (26) связаны с относительным движением частиц в системе. Они как раз представляют основной интерес в квантовохимических задачах, и о них далее будет идти более подробный разговор. И наконец, последний член в (25) или (26) отвечает так называемому кориолисову взаимодействию относительного движения с вращением системы. (Соответствующая сила, как известно еще со школьной скамьи, приводит к размыванию правого берега у рек, текущих с севера на юг.) Кориолисовым взаимодействием при начальном рассмотрении молекулярных задач также обычно пренебрегают.