Б. Отделение переменных центра масс

Как уже говорилось при рассмотрении задачи об атоме водорода, для свободной системы потенциалы взаимодействия частиц между собой не зависят от переменных центра масс системы, а полный импульс сохраняется, т. е. оператор импульса системы как целого коммутирует с оператором Гамильтона: PH = HP, где Р = у ра + у pt. a i.

Чтобы отделить переменные, отвечающие импульсу Р, введем так называемые координаты Якоби, причем сначала введем их для подсистем ядер и электронов отдельно. Если для ядер в исходной инерциальной системе координат радиусы-векторы обозначить как R_a, то далее можно линейным преобразованием перейти к следующим векторам:

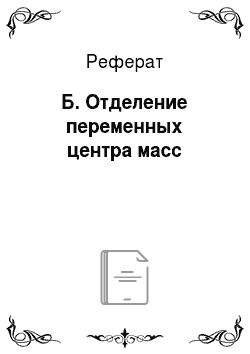
где _а (а = 1, 2,…, К-1) есть разность радиуса-вектора центра масс первых, а ядер и радиуса-вектора ядра с номером а+1, тогда как есть радиус-вектор Е центра масс подсистемы ядер (рис. 5.1.1). Оператор кинетической энергии ядер при этом будет иметь вид.

где, например, _Д?а =А—₊ JL_₊ А_ ^ Л/=?л/_а и ц_а ;

Рис. 5.1.1. Координаты Якоби для трех частиц.

постоянные, выражающиеся через массы ядер: pj^-1 = Л/,¹ + Л/г',.

Рг¹ = (Л/, + М₂)^-1 + А/;¹ и т. п.

Аналогично для электронов вводятся координаты.

где градиус-вектор /-го электрона, а Л — радиус-вектор центра масс подсистемы электронов. Оператор кинетической энергии подсистемы электронов будет иметь вид, аналогичный (6).

Наконец, от векторов ЗиЛ перейдем к их линейным комбинациям.

и.

Первая из них определяет радиус-вектор центра масс всей системы, вторая — относительное расположение центров масс подсистем ядер и электронов.

В новых переменных оператор Гамильтона приобретет вид.

где V_ee(tj) означает, что оператор V_ee зависит только от переменных аналогично У_пл(%) зависит только от переменных; тот же смысл имеют символы т| и ^ в обозначении оператора V_e«($, ip Ji). Кроме того, в этом выражении р^-1 = N'¹ + М'¹, т. е. рприведенная масса для двух подсистем: электронов и ядер.

От переменных центра масс зависит в выражении (10) для оператора Гамильтона лишь первое слагаемое, так что волновую функцию Ч*, собственную для //, можно искать в виде.

причем Р_х + Р* + Р₂² = 2(Л/ + N)E_tr, где E_tr — энергия поступательного (трансляционного) движения системы как целого, Р_х, Р_у и Р_т — постоянные компоненты импульса системы (собственные значения соответствующих операторов). Представление волновой функции Ч* в виде (11) позволяет выделить экспоненциальный множитель е'^РКцм, не обладающий интегрируемым квадратом модуля; оставшаяся же часть, т. е. функция ф (?, ц, X), для связанных состояний атомов и молекул интегрируемым квадратом модуля, вообще говоря, обладать уже должна: эта волновая функция, отвечающая покоящемуся центру масс (для нее Н_цм = 0), должна быть существенно отличной от нуля лишь в ограниченной, локализованной области пространства. При поиске приближенных выражений для гр (?, ц, X) это условие интегрируемости всегда имеет смысл учитывать, используя, например, в вариационном методе базисные функции, также имеющие интегрируемый квадрат модуля.

Естественно, можно было бы не вводить отдельно переменные центров масс ядер и электронов, а сразу ввести единую систему координат Якоби для всех частиц молекулы. Выше это сделано не было по следующей причине. В гамильтониане (10) после отделения переменных центра масс можно вместо трех независимых переменных X подставить три независимые переменные Л, что формально эквивалентно совмещению начала системы координат с центром масс ядер. Существенно подчеркнуть, что такая эквивалентность в действительности формальна, поскольку при этом центр масс всей системы полностью не отделяется, так что волновая функция должна была бы иметь сомножитель рассмотренного выше типа (e^/PR), причем в этой новой системе координат полный импульс системы уже не должен быть сохраняющейся величиной, а волновая функция — обладать интегрируемым квадратом модуля.

Введение

 же указанной подстановки проводится при условии, что она не меняет характера получаемого решения, и ищется такая волновая функция, которая интегрируемым квадратом модуля обладает. Найдя такое решение, в нем далее необходимо выделить переменные Л, заменить их на X, после чего полученная подобным образом функция и будет представлять собой искомую волновую функцию исследуемой молекулярной системы.

Что интересного дает обсуждаемая подстановка? Она позволяет вернуться в существенной степени к декартовым координатам электронов. Действительно, в гамильтониане (10) опера;

¹ л ¹ л 111.

тор — переходите—Д_Л, и коль скоро — = — + —, то.

• 2ц 2u it М N
• 111
• —Д_Л =—Д_Л—Д_Л. Второе слагаемое должно давать
• 2ц 2 N 2 М

существенно меньший вклад, поскольку М по крайней мере на три порядка больше N. Первое же слагаемое вместе с четвертым членом в гамильтониане (10) дает, где операторы Лапласа Дзаписаны в декартовых координатах. Кроме того, в выражении для потенциала V_en(^, ц, к) замена к на, А приводит вновь к декартовым переменным электронов, т. е.

^ven Поэтому гамильтониан (10), в котором переменные центра масс отделены и введена замена к на, А, приобретает вид:

I.

Последним членом при поиске собственных функций этого оператора можно на первых порах пренебречь, а далее учесть его как поправку, например по теории возмущений.

Все приведенные преобразования относятся к числу таких тонкостей, которые в настоящем тексте, при первом знакомстве с квантовой химией, может быть, и не стоило бы обсуждать. Упомянуто о них с единственной целью — показать, что даже в столь простых (казалось бы) местах квантовой теории молекул не все столь ясно и прозрачно, как может показаться на первый взгляд. Тем не менее, ниже столь подробно, как это только что сделано, на таких тонких вопросах теории останавливаться не будем, отмечая лишь при необходимости, что они существуют.