Разделяющие множества и разрезы

Рассмотрим конечный связный граф G (V, Е). Разделяющим множеством графа называется непустое подмножество Ej его ребер (?/ ?), удаление которых

(операция разборки вида 1) превращает его в несвязный суграф. Если граф G имеет по крайней мере две вершины, то разделяющее множество всегда существует (например,

Е,=Е).

Пример. На рис. 33 множество, состоящее из ребер а, Ь, с, d, е, f и g, является разделяющим множеством, так как их удаление разбивает граф на три компоненты связности G/, G2 и Gj (см. рис. 34).

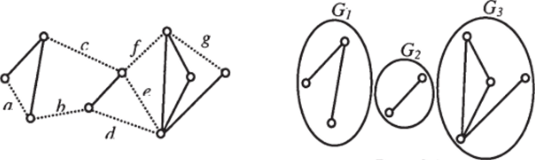
Рис. 34

Рис. 33

Пусть множество вершин конечного связного графа G (V, Е) разделено на два не пустых непересекающихся взаимно дополнительных подмножества W и W' (т.е. WnW' =0 и WUW' =V). Множество ребер графа G, соединяющих вершины из W с вершинами из W', называется разрезом, разделяющим W и W'. Так как при удалении всех ребер, входящих в разрез, граф становится несвязным, то любой разрез является разделяющим множеством. Обратное, вообще говоря, не верно. Так, например, разделяющее множество {a, b, с, d, е, /, g} (см. рис. 33) не является разрезом. Заметим, что подмножество, состоящее из ребер b, с, d, е, / образует разрез. Можно показать, что любое разделяющее множество содержит разрез в качестве своего подмножества.

Пусть G (V, E) — связный граф, содержащий по крайней мере две вершины. Тогда для любой вершины А

этого графа множество всех ребер, инцидентных вершине А, образует разрез.

Разделяющее множество называется простым разрезом, если оно является минимальным, т. е. не содержит собственного подмножества, разделяющего граф. Любой простой разрез является разрезом, но не всякий разрез является простым. Так, например, разрез {b, с, d, e, j) на рис. 33 не является простым разрезом, так как он содержит два собственных подмножества {Ь, с) и { d, e, f}, каждое из которых является разделяющим множеством (и простым разрезом).

Разделяющее множество, состоящее из единственного ребра, называется перешейком.

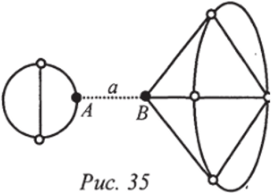
Ясно, что перешеек есть простой разрез. Примером перешейка является ребро а на рис. 35.

Легко видеть, что граничные точки любого перешейка всегда являются точками сочленения (точки А и В на рис. 35).

Перешейки и точки сочленения являются самыми узкими местами в графах транспортных сетей и наиболее сильно ограничивают их пропускную способность. Достаточно перекрыть всего один перешеек или всего одну точку сочленения, чтобы существенно парализовать сообщение.