Мультиграфы и псевдографы
Граф называется однородным {регулярным) степени к, если все его вершины имеют одинаковую степень к. Однородный граф нулевой степени называется нуль-графом или пустым графом. Он не имеет ребер и состоит только из изолированных вершин. Однородный граф третьей степени называется кубическим графом. В силу теоремы 1, любой однородный граф нечетной степени (в частности, любой кубический граф) содержит… Читать ещё >
Мультиграфы и псевдографы (реферат, курсовая, диплом, контрольная)
Конечный граф без петель называется мультиграфом. Он отличается от элементарного графа тем, что может содержать параллельные ребра. Наиболее общий случай графа, когда допускаются петли и параллельные ребра, называется псевдографом. В дальнейшем под термином «граф», если не сделано специальной оговорки, мы будем подразумевать наиболее общий случай псевдографа.
Однородные графы
Граф называется однородным {регулярным) степени к, если все его вершины имеют одинаковую степень к. Однородный граф нулевой степени называется нуль-графом или пустым графом. Он не имеет ребер и состоит только из изолированных вершин. Однородный граф третьей степени называется кубическим графом. В силу теоремы 1, любой однородный граф нечетной степени (в частности, любой кубический граф) содержит четное число вершин. Полный граф с п вершинами является однородным степени п-1, а полный граф с петлями — однородным степени п+1.
Двудольные и к-дольные графы
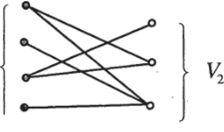
Конечный мультиграф называется двудольным или бихроматическим, если его вершины могут быть разделены на два непересекающихся подмножества V/ и V2 так, что каждое ребро имеет одну граничную точку в V), а другую в V2. Т. е. любое ребро графа не может соединять вершины из одного подмножества. Чтобы подчеркнуть это свойство двудольных графов, их обычно изображают, размещая множества вершин V/ и V2 в разных столбцах или строках (см. пример двудольного графа на рис. 18).
Двудольный граф называется элементарным, если он не содержит параллельных ребер (на рис. 18 предV, ставлен элементарный двудольный граф).
Элементарный двудоль- р ^
ный граф называется.
полным, если любая пара вершин из разных подмножеств соединена ребром (см. рис. 1). Полный двудольный граф содержит |Zs| = |V, | • |V2| ребер.
Аналогично определяется k-дольный граф при к > 2. Это такой мультиграф, вершины которого можно разделить на к непересекающихся подмножеств так, чтобы ребра не соединяли вершины из одного подмножества. Любой мультиграф с п вершинами можно рассматривать как и-дольный граф. Каждая его «доля» состоит всего из одной вершины. В частности, полный граф с п вершинами является n-дольным графом и не является-дольным графом для к < п.