Перепишем второй закон Ньютона (2.13) в виде.
где R — равнодействующая всех сил, действующих на тело. Это соотношение называется уравнением движения. В классической механике оно лежит в основе расчета любых движений. Уравнение (2.16) — это дифференциальное уравнение второго порядка. Оно может быть сведено к двум уравнениям первого порядка. Если ввести обозначение v = dx/dt, то (2.16) распадается на.
Рассмотрим отдельно случаи, когда R = 0, R = const 0, R * const.
Равномерное движение (R = 0)
Равномерным называется движение с постоянной скоростью v = const. В разделе 2 уже говорилось, что равномерное прямолинейное движение происходит в отсутствие каких-либо сил, действующих на тело. Реально этого никогда не бывает, всегда есть трение и другие силы. Это вовсе не значит, что равномерное движение тела возможно только в пустоте вдали от других тел, в отсутствие излучений и т. д. Наоборот, равномерное движение встречается в природе и используется в технике весьма часто. Для этого необходимо, чтобы равнодействующая R всех сил, действующих на тело, была равна нулю. При R = 0 из (2.17) ускорение dv/dt = 0, т. е. скорость неизменна. Тогда из второго уравнения (2.17) следует dx = vdt. Возьмем неопределенный интеграл (см. главу 1) от обеих частей этого равенства:
(постоянную v сразу выносим за знак интеграла). Получаем.
Вычислим значение произвольной постоянной из начальных условий. При? = 0 координата а: = х0. Тогда х = х0 + vt. Обозначая х — х, через S (пройденный путь), получаем.

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">
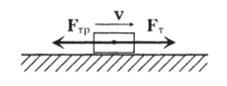
Рис. 2.15.
Обычно после короткого разгона автомобиль, морское судно, самолет и т. п. движутся равномерно, причем их скорость зависит от силы тяги двигателя. Происходит это потому, что сила трения в осях, сила сопротивления воздуха или воды зависят от скорости v, например по формуле (2.3) или (2.4) раздела 1 главы 2. Сначала при v = 0 сила трения тоже равна (или почти равна) нулю, но по мере нарастания скорости она увеличивается. Когда она сравнивается с силой тяги двигателя = F.f (рис. 2.15), равнодействующая становится равной нулю, а движение — равномерным.
Задачи на равномерное движение могут быть непростыми. Приведем примеры.
Пример 1. Рассмотрим равномерное движение поезда. С какой максимальной скоростью тепловоз, развивающий силу тяги 25 т, может вести состав массой 2000 т? Учесть трение по формуле (2.3). Коэффициенты равны А= 104 кг/с; В = 30 кгс/мг. Какую мощность при этом развивает тепловоз?

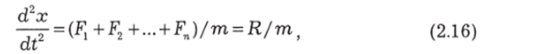

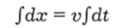

 aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">
aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">