Сложность алгоритмов. 
Основы программирования

Для сравнения алгоритмов принято использовать обобщенную характеристику, называемую эффективностью. Говорят, что алгоритм Л, эффективнее алгоритма А₂, если алгоритм Л, выполняется за меньшее время и (или) требует меньше компьютерных ресурсов (оперативной памяти, дискового пространства, сетевого трафика и т. п.).

Эффективный алгоритм должен удовлетворять требованиям приемлемого времени исполнения и разумной ресурсоемкое™, о чем уже упоминалось в параграфе 1.1. Совокупность этих характеристик составляет понятие сложности алгоритма. При увеличении времени исполнения алгоритма и (или) задействованных ресурсов сложность возрастает. Таким образом, понятия эффективности и сложности являются обратными один относительно другого.

Характеристика алгоритма, отражающая временные затраты на его реализацию, называется временной сложностью. Характеристика алгоритма, отражающая компьютерные ресурсные затраты на его реализацию, называется емкостной сложностью.

При количественной и качественной оценках алгоритма, связанных с определением сложности, используют два подхода — практический и теоретический.

Практический подход связан с реально выполняемыми алгоритмами на конкретных физических устройствах. Он характеризуется параметрами, которые можно измерить и зафиксировать. Временная сложность при таком подходе может выражаться во временных единицах (например, миллисекундах) или количестве тактов процессора, затрачиваемых на выполнение алгоритма. Емкостная сложность может выражается в битах (или других единицах измерения информации), минимальных аппаратных требованиях, необходимых для выполнения алгоритма, и пр.

Практическая оценка не является абсолютным показателем эффективности алгоритма. Количественные значения, получаемые при таком подходе, зависят от множества факторов, таких как:

• • технические характеристики компонент, составляющих вычислительную систему. Так, чем выше тактовая частота работы процессора, тем больше элементарных операций в единицу времени может быть выполнено;
• • характеристики программной среды (количество запущенных процессов, алгоритм работы планировщика заданий, особенностей работы операционной системы и т. д.);
• • выбранный язык программирования для реализации алгоритма. Программа, написанная на языке высокого уровня, скорее всего, будет выполняться медленнее и потребует больше ресурсов, нежели программа, написанная на низкоуровневых языках, имеющих непосредственный доступ к аппаратным ресурсам;
• • опыт программиста, реализовавшего алгоритм. Скорее всего, начинающий программист напишет менее эффективную программу, чем программист, имеющий опыт.

Таким образом, алгоритм, выполняемый в одной и той же вычислительной системе для одних и тех же входных данных, может иметь различные количественные оценки в различные моменты времени. Поэтому более важным оказывается теоретический подход к определению сложности.

Теоретическая сложность характеризует алгоритм без привязки к конкретному оборудованию, программному обеспечению и средствам реализации. В этом случае временная сложность выражается в количестве операций, тактах работы машины Тьюринга и т. д. Емкостная сложность определяется объемом данных (входных, промежуточных, выходных), числом задействованных ячеек на ленте машины Тыоринга и т. д.

При теоретическом подходе к оценке эффективности считается, что алгоритм выполняется на некотором идеализированном компьютере, для которого время выполнения каждого вида операций известно и постоянно. Также считается, что ресурсы такого компьютера бесконечны, поэтому емкостную сложность при теоретическом подходе обычно не определяют. В качестве временной характеристики сложности выбирают количество инструкций (операций), выполняемых на идеализированном компьютере.

Количественные оценки, получаемые при теоретическом подходе, также могут зависеть от ряда следующих факторов:

• • объем входных данных. Чем он больше, тем больше времени потребуется на выполнение алгоритма;
• • выбранный метод решения задачи. Например, для большого объема входных данных алгоритм быстрой сортировки эффективное, чем алгоритм пузырьковой сортировки, хотя и приводит к такому же результату.

Время выполнения алгоритма обычно зависит от объема входных данных (размер входа), под которым понимают размерность решаемой задачи. Так, при сортировке множества значений объем данных составляет количество элементов этого множества. При обработке строк объемом входных данных считается длина строки.

Пусть п — объем входных данных для некоторого алгоритма. Обозначим за Т (п) количество инструкций, выполняемых на идеализированном компьютере при исполнении алгоритма, причем оно определяется для «наихудшего случая», когда объем операций максимален.

Понятие «наихудшего случая» можно проиллюстрировать на примере. Пусть рассматривается алгоритм проверки наличия числового элемента в некотором множестве (массиве) чисел. Если это множество упорядочено по возрастанию, то, вообще говоря, нет смысла проверять элементы, расположенные после первого элемента, который больше искомого. В этом случае Т (п) < п. Однако в наихудшем случае (для произвольного несортированного множества) придется просмотреть все элементы множества. Очевидно, здесь Т (п) = п.

Вообще говоря, Т (п) является некоторой функцией от объема входных данных п. Во многих случаях Т (п) выражается полиномиальной, степенной или логарифмической функцией от п.

Поведение величины Т (п) в зависимости от увеличения п называют асимптотической сложностью алгоритма. Говорят, что Т (п) имеет порядок сложности 0(J (n)) (читается «О большое от/от п») для некоторого алгоритма, если существуют константа с и объем данных щ такие, что Уп > п₀ и имеет место неравенство Т (п) < с/(п).

Данный факт записывается как Т (п) = 0(J (n)) и означает, что для функции Т (п) существуют такая функция f (n) и константа с, для которых, начиная с некоторого п₀, значение Т (п) не превосходит cf (n).

Функция f (n) представляет собой верхнюю границу значений функции Т (п). Пусть, например, Т (п) = 2п^А + п². Выбрав значения п₀ = 0 и с = 5, для любого п > п₀ имеем Т (п) = 2п^А + п² < 5гг⁴, следовательно, Т (п) имеет порядок я⁴.

Важно!

Функция Т (п) связана с определенным алгоритмом, поэтому часто говорят, что порядок сложности 0(/(п)) имеет именно алгоритм.

Говорят, что Т (п) имеет нижнюю границу Q (g (n)) (читается «омега большое от g от /г»), если существуют константа с и объем данных п₀ такие, что /п и имеет место неравенство Т (п) > cg (n).

Данный факт записывается как Т (п) = Q (g (n)). Пусть, например, Т (п) = 2я⁴ + п². Выбрав значение с = 1, для любого п имеем Т{п) = 2я⁴ + п²> сп^А> следовательно, Т (п) имеет нижнюю границу я⁴.

Важно!

Нетрудно видеть, что порядок и нижняя граница не являются единственными для некоторой функции Т (п). В примерах выше в качестве /(я) можно было выбрать я⁵, я⁶,…, а в качестве g (n) — я³, я²,… Обычно в качестве /(я) выбирают функцию с минимальной степенью, а в качестве g (n) — с максимальной.

Порядок сложности 0(/(я)) и нижняя граница Q (g (rc)) представляют собой классы функций. Интуитивно Q (g'(n)) можно понимать как класс функций растущих по крайней мере так же быстро, как и Т (п). Аналогично, интуитивно 0(f (n)) можно понимать как класс функций, растущих не быстрее, чем Т (п). С практической точки зрения при оценке сложности алгоритма наиболее важным оказывается именно класс функций 0(f (n)). Определение вида функции /(я) и является основной задачей расчета теоретической сложности алгоритма.

Для любого алгоритма при определении степени роста можно воспользоваться следующими свойствами 0(/(я)):

1) 0(kf (ji)) = 0(/(я)), где k = const. Таким образом, постоянный множитель в функции не оказывает влияние на скорость роста. Например,.

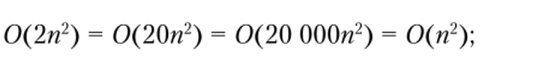
2) 0(J (ri)'g (n)) = 0(J (n))'0(g (ri)). Таким образом, порядок произведения двух функций равен произведению их сложностей. Например,.

Иногда это свойство записывают как.

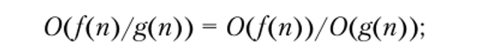
3) 0(/(п) + g (n)) равен доминанте (функции с максимальной степенью) функций /(я) и g (n). Например,.

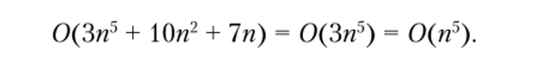
В теории сложности алгоритмов выделяют следующие классы функций сложности:

• 1) константная сложность 0(1). Время работы алгоритма и используемые ресурсы не имеют зависимости от объема входных данных. Обычно такую сложность имеют алгоритмы, не содержащие циклов и рекурсивных вызовов;
• 2) линейная сложность 0(п). Обычно такую сложность имеют задачи, в которых каждый элемент входных данных должен быть обработан определенное количество раз, никак не связанное с количеством обработок других элементов;
• 3) логарифмическая сложность 0(log₂w), 0(nog₂n). Иногда используются и другие основания логарифма;
• 4) полиномиальная сложность 0(я²), 0(/г³), 0(я⁴),…;
• 5) экспоненциальная сложность 2^п, 3″ ,…

При увеличении размера входа сложность каждого последующего типа функций растет быстрее, чем предыдущего (кроме 0(log₂/?)). Для достаточно большого объема входных данных предпочтительнее использовать алгоритмы с меньшей сложностью.

При количественном подсчете сложности первоначально выбирают операцию или группу операций, которая значима для этого алгоритма (составляет его основу). В их качестве обычно выступают операции сравнения и арифметические операции. К операциям сравнения относят проверку значений двух величин (меньше, больше, равно, меньше или равно, больше или равно, не равно). Они считаются эквивалентными по времени выполнения. Арифметические операции, в свою очередь, делят на аддитивные и мультипликативные. К первым (часто называемым просто сложением) относят сложение, вычитание, уменьшение или уменьшение значения счетчика. Ко вторым (называемым просто умножением) относят умножение, деление, взятие остатка по модулю.

Операции сложения выполняются быстрее, чем операции умножения, поэтому алгоритмы с меньшим количеством умножений являются предпочтительными, даже если количество сложений растет пропорционально количеству уменьшения умножений.

Операции целочисленного умножения или деления па степень числа 2 относят к аддитивным операциям, так как при работе с ячейками памяти они сводятся к сдвигу, который эквивалентен операции сложения.

После выбора значимых операций они делятся на две категории:

• 1) операции, непосредственно влияющие на сложность алгоритма;
• 2) операции, составляющие «накладные расходы» при выполнении алгоритма (например, выделение памяти для хранения промежуточных данных).

Непосредственный подсчет или оценка количества выполняемых операций позволяет оценить Т (п).

Для оценки порядка сложности можно использовать анализ программного кода, реализующего алгоритм. При этом:

• • алгоритмы без циклов и рекурсивных вызовов имеют сложность порядка 0(1). Таким образом, операции присваивания, ввода и вывода данных, условные конструкции имеют константную сложность;
• • если две части программного кода имеют сложности 0(J_{(ri)) и 0(J₂(n)), то последовательное выполнение имеет сложность

о (/"+Л (к";

• • если тело цикла выполняется один раз для каждого элемента входных данных, то сложность выполнения цикла имеет порядок 0(п)0( 1) = 0(п);
• • порядок сложности выполнения вложенных циклов вычисляется по правилу произведения 0(J_x(n)f₂(n)) = 0(/,(/?)) — 0(J₂(ri)). Если каждый из них имеет сложность порядка 0(п), выполнение вложенных циклов имеет сложность порядка 0(п²).

Пример 1.3

Определить порядок сложности алгоритма программы на языке.

Pascal, приведенного в листинге 1.2. Строки программы пронумерованы в виде комментариев (см. параграф 2.6).

Листинг 1.2

{01} for i:=l to n do

{02} begin

{03} write ('Введите элемент массива

с индексом ', i,': ');

{04} Readln (MyArray[i]);

{05} end;

{06} for i:=l to n do

{07} for j:=1 to n do

{08} begin

{09} write ('Введите элемент массива

с индексами ', i, ',', j, ': ');

{10} Readln (МуDArray[i, j]);

{11} end;

Решение

Строки 02, 05, 08, 11 не содержат исполняемых операторов, поэтому при определении порядка они не учитываются.

Строки 03 и 04 имеют порядок 0(1). Последовательное их выполнение имеет порядок 0(1) + 0(1) = 0(1). Аналогично, последовательное выполнение строк 09 и 10 имеет сложность 0(1).

Цикл в строках 01—05 имеет сложность порядка О (п), вложенные циклы в строках 06—11 — порядка 0(п²). Итоговая сложность алгоритма имеет порядок.

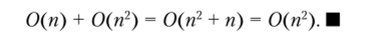
Оценка сложности алгоритма, как временной, так и ресурсной, позволяет определить максимальное и среднее время исполнения алгоритма. Это крайне важно при обработке больших массивов информации, особенно в задачах сортировки и поиска, рассмотренных далее.