Вещественные числа. 
Математика в экономике

Поскольку, как уже говорилось во введении, мы изучаем аксиоматическую математику, необходимо строго определять объекты, с которыми мы оперируем, а также их свойства.

Вилы и свойства вещественных чисел

Множество вещественных чисел является бесконечным. Оно состоит из рациональных и иррациональных чисел. Рациональным называется число вида p/q, где р и q — целые числа. Всякое вещественное число, не являющееся рациональным, называется иррациональным. Всякое рациональное число либо является целым, либо представляет собой конечную или периодическую бесконечную десятичную дробь. Например, рациональное число 1/9 можно представить в виде 0,11 111… Иррациональное число представляет собой бесконечную непериодическую десятичную дробь; примеры иррациональных чисел: >/2= 1,41 421 356…, п = 3,14 159 265…

Перечислим свойства вещественных чисел.

I. Сложение и умножение вещественных чисел Для любой пары вещественных чисел а и b определены единственным образом два вещественных числа а + ЬнаЬ, называемые соответственно их суммой и произведением. Для любых чисел а, b и с имеют место следующие свойства.

• 1. а + b = b + a_t ab = Ьа (переместительное свойство).
• 2. а + (Ь + с) = (а + b) + с, a (bc) = {ab)c (сочетательное свойство).
• 3. (а + Ь)с = ас + Ьс (распределительное свойство).
• 4. Существует единственное число 0, такое, что а + 0 = а для любого числа а.
• 5. Для любого числа а существует такое число (-а), что а + (-а) = 0.
• 6. Существует единственное число 1 * 0, что для любого числа а имеет место равенство al — а.
• 7. Для любого числа а ф 0 существует такое число а~ что ааг¹ = 1 Число

аобозначается также символом -.

а

II. Сравнение вещественных чисел Для любых двух вещественных чисел установлено одно из трех соотношений: а — b (а равно b)> а > b (а больше Ь) или а < b (а меньше Ь). Отношение равенства обладает свойством транзитивности: если а = ЬЬ = с, тоа = с.

Для любых чисел a_tbc отношение «больше» обладает следующими свойствами.

• 8. Если а > b и b > с, то а > с.
• 9. Если а > Ь, то а + с > b + с.
• 10. Если а > 0 и b > 0, то ab > 0.

Вместо соотношения а > b употребляют также соотношение b < а. Запись а? b (Ь? а) означает, что-либо а = Ь> либо а > Ь. Соотношения со знаками >, и < называются неравенствами, причем соотношения типа 8—10 — строгими неравенствами.

11. Любое вещественное число можно приблизить рациональными числами с произвольной точностью.

Для определенности будем считать это число неотрицательным и представим его в виде бесконечной дроби а = а₀, a_ia₂a_y.a_n… . Обрывая эту дробь на л-м знаке после запятой, получим рациональное число a_Q, а^а₂…а_п. Увеличим его на 1/10″. Тогда справедливо двойное неравенство:

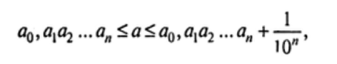
т.с. число, а заключено между двумя рациональными числами. Поскольку н можно взять любым, мы получаем справедливость исходного утверждения.

III. Непрерывность вещественных чисел.

12. Пусть X и У — два множества вещественных чисел. Тогда, если для любых чисел х е X и у е Y выполняется неравенство х < у, то существует хотя бы одно число с, такое, что для всех х и у выполняются неравенства х < с < у.

Свойством непрерывности обладает множество всех вещественных (действительных) чисел, но не обладает множество, состоящее только из рациональных чисел.

Из основных свойств I —111 вещественных чисел вытекают все остальные их свойства, в том числе известные из курса школьной математики. Можно определить, что вещественные числа п ре дета вл я ют собой множество элементов, обладающих свойствами I—111. Такое определение, из которого выводятся остальные свойства, называется аксиоматическим, а сами свойства I—III — аксиомами вещественных чисел.