Задача о замене оборудования

Ценность рассмотренных ранее задач состоит не только в их важном прикладном значении, но и в том, что многие другие реальные задачи, содержательно совершенно не связанные с условиями перечисленных задач, имеют аналогичные ММ и могут быть решены наиболее эффективными методами.

Пример такого типа задачи ;

Задача о замене оборудования.

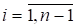
Пусть промышленное предприятие функционирует в течение некоторых промежутков времени с номерами. Для выполнения производственной программы предприятие арендует необходимое оборудование. Через какие-то промежутки времени оборудование заменяется на новое. Если оборудование эксплуатируется в промежутке времени (i, j), т. е. начинается эксплуатация в начале i-того периода и заменяется в начале j-того промежутка времени, то предприятие несет затраты (на аренду, тех. обслуживание, ремонт и т. п.).

Необходимо определить, в начале каких промежутков времени нужно заменять оборудование, чтобы суммарные затраты в течение рассматриваемых промежутков времени были бы минимальны.

Всевозможные случаи замены оборудования можно изобразить с помощью ориентированного графа:

Здесь узлы графа соответствуют номерам начала периодов. Если оборудование эксплуатируется в течение промежутка (i, j), то на графе ставится соответствующая дуга, взвешенная числом. Оборудование арендуется в начале 1-го периода, а процесс функционирования предприятия завершается в начале периода времени n.

Допустим, в процессе эксплуатации оборудование заменяется при i=2 и i=7, т. е. оборудование заменяется в начале первого, второго и седьмого периодов: и эксплуатируется до узла n. Тогда, очевидно, общая сумма затрат будет равна. А это выражение есть ни что иное, как длина пути (1,2,7,n).Таким, образом, каждому варианту замены оборудования можно поставить в соответствие некоторый путь из узла 1 в узел n. Т. е. множество вариантов замены оборудования отражается множеством путей на рассматриваемом графе. Следовательно, задача оптимального плана замены оборудования эквивалентна задаче поиска кратчайшего пути из узла 1 в узел n на рассматриваемой сети. (Предложить студентам записать ММ самостоятельно.)

Одна задача календарного планирования трудовых ресурсов.

Рассматривается функционирование предприятия в условиях сурового климата, его производственная программа может быть связана дополнительно с сезонностью. В таких условиях предприятию невыгодно создавать постоянные производственные коллективы и соответствующую социально-экономическую инфраструктуру.

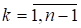
Пусть рассматривается функционирование предприятия в течение n-1 промежутка времени, причем известно потребное количество бригад рабочих Rk () для выполнения производственной программы в течение к-того промежутка времени (периода). Если одна бригада рабочих на7имается в начале i-того промежутка и увольняется в начале j-того, т. е. используется в интервале (i, j), то затраты на содержание этой бригады равны .

Необходимо найти план найма и увольнения бригад, при котором в каждом промежутке времени должен выполняться заданный объем работ, а суммарные затраты на содержание бригад минимальны.

Всевозможные варианты найма и увольнения бригад можно изобразить в виде сети, в которой дуга (i, j) означает найм в начале i-того и увольнение в начале j-того периода.

Построение ММ.

Пусть — количество бригад, нанимаемых в начале i-того и увольняемых в начале j-того промежутков. Тогда ММ запишется:

.

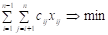
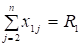
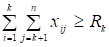
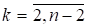
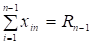
— целые В модели целевая функция (1) отражает суммарные затраты на содержание рабочих бригад. Ограничение (2) требует, чтобы в первом промежутке времени было ровно столько бригад, сколько требуется для выполнения работ на первом промежутке времени. Неравенство (3) допускает целесообразность содержания резервных бригад, т.к. они могут в конечном счете обойтись дешевле. Равенство (4) обеспечивает в последнем промежутке наличие ровно стольких бригад, сколько требуется. Условие (5) вытекает из физического смысла.

Модель (1)-(5) относится к классу задач линейного целочисленного программирования. Однако она тождественными преобразованиями сводится к модели транспортной задачи в сетевой постановке.

Неравенство (3) приводится к равенству введением доп. переменных:

.

.

Идея последующих тождественных преобразований заключается в следующем: из уравнений (7) и (4) соответственно вычитаем уравнения (2) и (7), записанные для участка с номером на единицу меньше. Запишем уравнение (7) для участка с номером к-1:

.

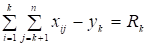
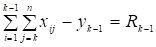
Далее, вычтем (8) из (7):

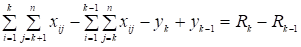
и =.

.

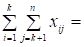
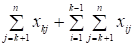
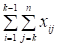
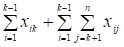
Проведя сокращения, можно записать:

.

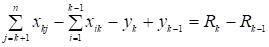
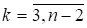
Если вычесть из уравнения (7) с номером к=2 уравнение (2), то получим: ориентированный календарный транспортный сетевой.

.

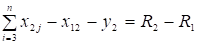
Теперь из уравнения (4) вычтем уравнение (7) с номером. Т.к. уравнение (4) аналогично (7) при и, то результат вычитания следует из формулы (9) при :

.

К полученной системе уравнений (9)-(11) присоединим уравнения (2) и (4), умножив (4) слева и с права на -1:

.

.

Полученные уравнения (9)-(13) эквивалентны уравнениям исходной задачи, которая теперь свелась к задаче (1), (9)-(13) с условиями.

.

— целые Далее можно условно интерпретировать:

— объем перевозки по дуге (i, j).

R1— запас продукции в первом узле,.

RкRк-1 — запас продукции k-того узла ,.

Rn-1 — запас продукции n-ого узла.

Тогда уравнение (12) интерпретируется как объем вывоза из первого узла, равный запасу продукции в этом узле, т. е. аналогично уравнению для истока транспортной сети. Уравнение (13) интерпретируется как объем продукции, привозимой в размере потребности в узел n, т. е. аналогичное уравнению для стока транспортной сети.

Рассмотрим уравнение (10):

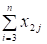
— определяет объем продукции, вывозимый из узла 2,.

— объем продукции, ввозимый в узел 2 по дуге (1,2).

В сеть вводится дополнительная дуга (3,2), по которой перевозится продукция в объеме. Тогда — суммарный объем продукции, привозимой в узел 2. Следовательно уравнение (10) можно интерпретировать как уравнение баланса для промежуточных узлов транспортной задачи в сетевой постановке.

Аналогично в сеть добавляются дуги (k, k-1) для всех с объемами перевозок .

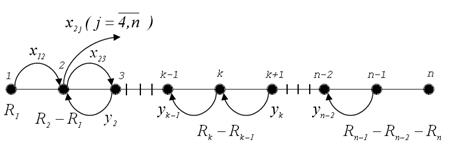
Тогда уравнения (9) интерпретируются как уравнения баланса для промежуточных пунктов ТЗ в сетевой постановке: суммарный объем вывозимой продукции минус суммарный объем ввозимой продукции равняется запасу продукции в этих узлах.

Таким образом, задача календарного планирования трудовых ресурсов (1)-(5) тождественными преобразованиями и добавлением новых дуг свелась к модели транспортной задачи в сетевой постановке (1), (9)-(13).