Понятие непрерывности фуншии

Определение непрерывности функции

Понятие непрерывности функции является фундаментальным в математическом анализе.

Пусть функция / (х) определена в некоторой окрестности точки а.

Определение 9. Функция/(х) называется непрерывной в точке а, если предел этой функции и се значение в этой точке равны, т. е.:

Так как lim х = я, это равенство можно переписать в следующей форме:

х->а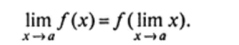

Определение непрерывности функции можно сформулировать как «на языке последовательностей», так и «на языке е — 8» в соответствии с двумя определениями предела функции в точке. Приведем здесь второе из них.

Определение 10. Функция /(х) называется непрерывной в точке л, если для любого е > 0 существует 8 > 0, такое, что при всех х, удовлетворяющих неравенству |х — а < 8, выполняется неравенство |/(х) — /(а)| < е.

Определение II. Функция / (х) называется непрерывной справа (слева) в точке я, если правый (левый) предел этой функции в точке а равен значению функции в этой точке.

Символическая запись непрерывности функции справа (слева):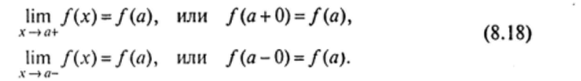

Если функция/(л:) непрерывна в точке а слева и справа, то она непрерывна в этой точке. В самом деле, в силу теоремы 8.2 предел функции/(а) о точке а равен ее значению в этой точке.

Для практического использования полезно сформулировать еще одно определение непрерывности функции. Назовем разность Да: = а — а приращением аргумента в точке о, а разность Ду = f (x) — f{a) — приращением функции в точке а, обусловленным приращением аргумента Ах. Таким образом,.

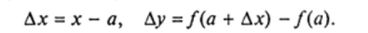aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

Поскольку условия х->аих-а->0 равносильны, равенство (8.17) можно переписать в другой форме:

Геометрическая интерпретация приращений Да* и Ду показана на рис. 8.7.

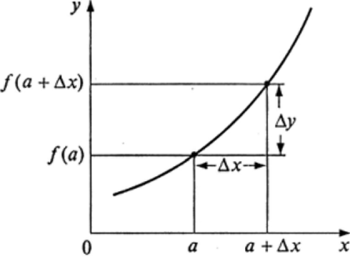
Рис. 8.7.

Равенство (8.19) представляет собой еще одно определение непрерывности функции в точке.

Определение 12. Функция/(а) называется непрерывной в точке а, если ее приращение в этой точке является бесконечно малой при Да -" 0.

Точки, в которых функция не является непрерывной, называются точками разрыва функции.

Рассмотрим наиболее яркие примеры точек, в которых функция нс является непрерывной.

• 1. Функция /(а) = sign, а (см. п. 8.1.2). Как было показано ранее, в точке, а = 0 существуют левый и правый пределы этой функции, равные соответственно -1 и +1. Сама же точка, а = 0 является точкой разрыва функции, поскольку пределы слева и справа не равны значению /(0) = 0.
• 2. Функция Дирихле (см. п. 8.1.2). Эта функция нс является непрерывной ни в одной точке области своего определения. Действительно, в любой окрестности произвольной точки а содержится бесконечно много рациональных и иррациональных значений аргумента, при которых функция принимает соответственно значения +1 и -1. Следовательно, условие непрерывности
• (8.19) нс выполняется.

Арифметические действия нал непрерывными функциями

Теорема 8.9. Пусть функции /(х) и g (x) непрерывны в точке а. Тогда функции /(х) ± ?(х),/(х) #(х) и /(x)/g (x) также непрерывны в точке а (частное при условии ?(л) * 0).

Доказательство. Поскольку непрерывные в точке а функции /(х) и g (x) имеют в этой точке пределы, равные соответственно /(а) и g (а), по теореме 8.3 пределы функций f (x) ± g (x), /(a) g (х) и f (x)/g(х) также существуют и равны соответственноf (a) ±g (a), f (a) g (a) и f (a)/g (a). Но эти величины равны значениям соответствующих функций в точке а. Следовательно, в силу определения 2, функции fix) ± g (x)_tf{x)g (x) и f (x)/g (x) непрерывны в точке я, что и требовалось доказать. ?