Линейные дифференциальные уравнения первого порядка

Определение 7. Уравнение вида.

где р (х) и q (x) — непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Неизвестная функция и ее производная входят в указанное уравнение в первой степени — линейно, что и объясняет название уравнения.

Если q (x) s 0, то уравнение (18.9) называется линейным однородным; если же функция q (x) не равна тождественно нулю, то уравнение (18.9) называется линейным неоднородным.

Пусть линейное однородное уравнение.

соответствует неоднородному уравнению (18.9). Мы рассмотрим так называемый метод вариации постоянной — метод решения неоднородного уравнения.

• (18.9), основанный на предварительном решении однородного уравнения
• (18.10). Уравнение (18.10) можно решить методом разделения переменных:

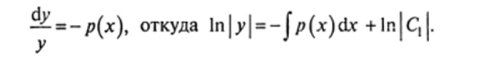aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

Потенцируя, получаем общее решение уравнения (18.9): где С = ±С,.

Общее решение уравнения (18.9) ищем в виде (18.11), полагая С новой неизвестной функцией от аргумента х:

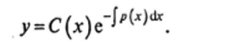
Подставим решение (18.11) в уравнение (18.9) с тем, чтобы найти функцию С (х); имеем: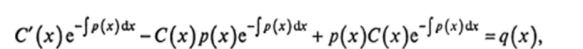

откуда после приведения подобных получаем уравнение для С (х):

Интегрирование уравнения (18.12) дает выражение для С (х):

подстановка которого в формулу общего решения (18.11) приводит к окончательному виду решения неоднородного уравнения (18.9):

Отметим, что некоторые нелинейные уравнения приводятся к линейным уравнениям соответствующими заменами неизвестной функции у{х). К таковым нелинейным уравнениям относится уравнение Бернулли:

где р и q — непрерывные функции, а п — некоторое постоянное число. При п = 0 имеем линейное неоднородное уравнение, а при п = 1 — линейное однородное уравнение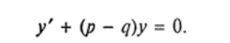

Пусть /I * 0, п *? 1. Введем новую функцию.

тогда Поделив обе части уравнения (18.14) на yⁿ_t получаем.

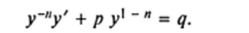
Умножая обе части этого уравнения на (I — я), с учетом выражений для новой функции z и ее производной получаем линейное дифференциальное неоднородное уравнение относительно неизвестной функции z (x):

В этом уравнении, метод решения которого нам известен, функция z (x) связана с искомой функцией у (х) соотношением (18.15).

Рассмотрим решение неоднородных уравнений первого порядка на примерах.

Пример 8. Найти общее решение уравнения у' + х²у = х².

Решение. Это линейное неоднородное уравнение первого порядка. Сначала решим соответствующее ему однооодное уоавнение.

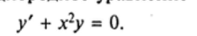
Разделяя переменные, получаем:

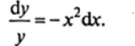
У.

Интегрирование левой части этого уравнения по у и правой — по х даст решение однородного уравнения:

Полагая С функцией отх и подставляя найденное решение в исходное неоднородное уравнение, получаем после приведения подобных дифференциальное уравнение для С (х):

После интегрирования этого уравнения и подстановки в уже найденное решение однородного уравнения получим искомое решение исходного уравнения:

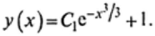
Пример 9. ху' + у = с*.

Решение. Опять начинаем с однородного уравнения.

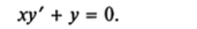
Разделяя переменные, получаем после интегрирования его решение:

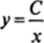
Полагая, что С= С (х), после подстановки в неоднородное уравнение получаем: Стало быть, общее решение исходного уравнения имеет вид:

Пример 10. у'+ ху = ху*.

Решение. Данное нелинейное уравнение представляет собой уравнение Бернулли при п- 3. Заменой искомой функции z = y~² согласно уравнению (18.16) получим линейное неоднородное уравнение относительно г (*):

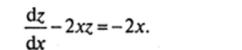
По формуле (18.12) получаем общее решение этого уравнения:

Теперь, выполняя обратную замену у = ±/yfz, получаем решение исходного нелинейного уравнения: