Вывод формулы EOQ

Рассмотрим последовательность вывода формулы EOQ для одного цикла (первый подход). В этом случае зависимость суммарных затрат (5.1) можно представить в виде.

где С_с — суммарные затраты на закажи хранение за цикл, руб.; С₀ — затраты на выполнение одного заказа, руб.; Q — средняя величина текущего запаса за цикл, ед.; h — затраты на хранение единицы продукции в день, руб/ед. х х день; Т — продолжительность одного цикла, дн.

Для определения Q сначала выведем уравнение для расхода запаса Q (t) за цикл. Поскольку для модели EOQ принято, что интенсивность расхода постоянна, т. е. X = const, запишем дифференциальное уравнение для расхода запаса в виде или.

Проинтегрировав уравнение (5.7), находим Подставив начальные условия Q (t = 0) = Q, получим.

Для определения величины среднего запаса за цикл воспользуемся формулой.

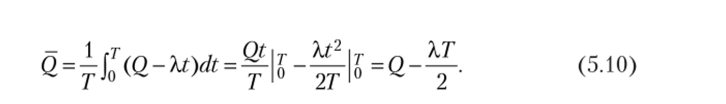
Учитывая, что Q = XT, находим Q = Q / 2. Следовательно,.

При подстановке (5.11) в формулу (5.5) получим.

Введем удельные затраты за цикл С_у = С_с/ Q. Под удельными затратами понимаются расходы по формированию и содержанию единицы запаса за цикл поставки. Таким образом, критериальное уравнение для определения оптимальной величины заказа записывается в виде.

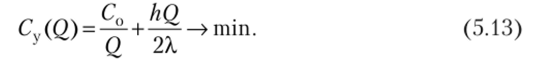
Для определения минимального значения функции C_V(Q) воспользуемся известной процедурой: возьмем первую производную и приравняем ее нулю:

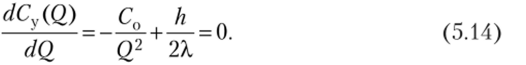
Из уравнения (5.14) находим оптимальную величину заказа.

Определим параметры, характеризующие модель EOQ.

• длительность цикла поставки (периода времени между поставками)'.

Рассмотрим второй подход. Домножив зависимость (5.12) на число циклов за период Д, получим.

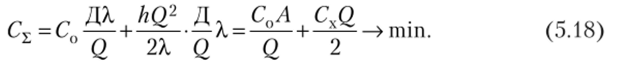
Выполнив преобразования, аналогичные (5.14), находим оптимальную партию заказа.

Что касается затрат С_х, связанных с хранением, то наиболее распространенная зависимость записывается в виде.

где С" — цена единицы продукции, хранящейся на складе, руб.; / — доля от цены C_w приходящаяся на затраты по хранению.

Остальные показатели модели EOQ:

• количество циклов'.

При подстановке (5.20) в формулу (5.19) получим так называемую формулу Уилсона (наиболее распространенное название):

продолжительность цикла:

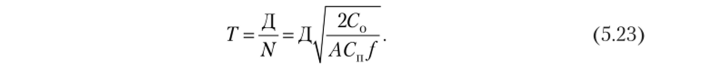
Определим величину минимальных общих затрат C_?min. Подставим Q, в зависимость (5.18) для Су, получим.

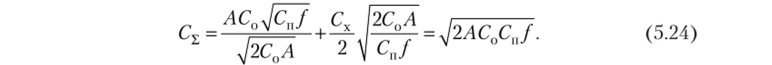
Формула (5.21) встречается в различных источниках под следующими названиями: формула Уилсона (Вильсона), Харриса, Кампа, Боуля — Тобина (финансовый менеджмент). Самым распространенным является первый вариант названия, однако существует дискуссия по поводу авторства данной формулы. Изучив историю формулы, мы пришли к выводу, что формула оптимального размера заказа может называться формулой Харриса — Уилсона.

? Научная дискуссия¹

Согласно американским источникам, в 1915—1922 гг. несколько авторов (Р. Дэвис, Г. Оуэн, В. Вилсон, В. Миллер, Дж. Пеннигтон, Г. МакГилл, Ф. Кларк, Дж. Медлен), действуя независимо друг от друга, получили формулу для наиболее экономичного размера партии, минимизирующего общие издержки хранения товара для случая, когда спрос известен и является постоянной величиной. Существует мнение, что время появления модели оптимального размера заказа (партии поставки) и вывод формулы EOQ, получившей название «формулы Уилсона», датируется в пределах от 1916 г. до 1934 г., когда была опубликована его статья.

Считается, что в 1913 г. Форд Харрис также вывел формулу экономичного размера партии при планировании запасов незавершенного производства. Согласно проведенным исследованиям (Operation Research Society of America, 1990), зависимость общих затрат в работе Ф. Харриса была записана так:

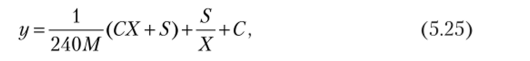
¹ Лукинскии В. С., Лукинский В. В., Плетнева Н. Г. Логистика и управление цепями поставок.

где М — ежемесячное потребление продукции, ед.; С — стоимость единицы продукции; S — затраты, связанные с организацией заказа; X — искомая партия заказа, ед.

Величина 240, входящая в формулу (5.25), включает в себя 2 • 12 / i, где i — доля от стоимости продукции, приходящаяся на затраты по хранению; при этом принято, что i = 0,1. После несложных преобразований, аналогичных (5.14), получим.

Следовательно, Форд Харрис сформулировал модель для расчета оптимального размера заказа раньше, чем Р. Уилсон, и при оценке затрат на хранение учитывал среднюю величину заказа. Справедливости ради следует подчеркнуть, что в своей статье он не приводит формулу для Х_опт, а только описывает ее словами, а именно: «The value for X that will give the minimum value to Y, reduces to the square root of (240MS divided by C)»^{ («Значение X, при котором Y принимает минимальное значение, определяется как корень квадратный из выражения (240MS, деленного на С)»).

Однако А. П. Долгов^[1][2] приводит совсем другую трактовку вывода формулы (5.26), согласно которой Ф. Харрис получил аналитическую зависимость для расчета экономичного размера партии незавершенного производства в 1913 г. в следующем виде:

где Р — затраты по подготовку обработки партии деталей (изделий); S — дневной темп (интенсивность) выпуска; С — себестоимость единицы продукции; К — постоянная, в которую входят такие слагаемые, как процент на капитал, складские расходы, страховые взносы, налоги и пр.

Профессор Долгов полагает, что формула производственного запаса достаточно близка по своему виду к выражению (5.26), но все же имеет некоторые различия. Попытаемся в них разобраться. Запишем формулу (5.27) в виде.

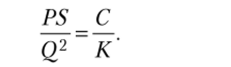
После интегрирования получим.

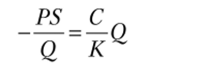
или, возвращаясь к общим затратам, няя величина запаса в формуле (5.25) равнаQ, тогда как в формуле (5.28).

она принимается пропорциональной Q; в-третьих, в анализируемых формулах используются различные подходы к учету составляющих затрат.

Нетрудно заметить, что, во-первых, зависимость (5.25) включает четыре параметра (С, X, S, г), а зависимость (5.28) — пять (Р, S, С, Q, К); во-вторых, средТак, в формуле (5.25) Ф. Харрис, по существу, впервые ввел добавленную стоимость которая суммируется с затратами на хранение. ?

Модель EOQ встречается в работах многих специалистов по логистике и управлению запасами как в нашей стране, так и за рубежом. В некоторых работах данная модель — единственная формула, которую могут увидеть читатели. В большинстве работ исследования в области определения оптимальной партии заканчиваются приведением формулы и примера расчета по ней. Проанализируем влияние составляющих модели EOQ на получаемый результат и оценим устойчивость модели.

? Научная дискуссия.

• [1] Цит. по: Harris F. W. How many parts to make at once // Operations Research. 1990.Nov. — Dec. Vol. 38. № 6. P. 947−950.
• [2] Долгов Л. П. Модель EOQ в историческом разрезе: проблема идентификации авторстваформулы // Логистика сегодня. 2006. № 5. С. 270—282.