Теплоотдача при вынужденной конвекции в трубах

Движение жидкости в данной системе под действием неоднородного поля массовых сил, приложенных к частицам жидкости внутри системы, обусловленное внешними полями (гравитационным, магнитным, электрическим), называют свободным движением или свободной конвекцией.

Свободное движение под действием гравитационного поля в системе с неоднородным распределением плотности жидкости (вызвано неоднородным распределением температуры, концентрации какого-либо компонента в смеси или наличием фаз с разной плотностью) называют гравитационным свободным движением или гравитационной свободной конвекцией.

Перенос теплоты, происходящий при обтекании твердого тела потоком жидкости при ее свободном движении, называют теплоотдачей при свободном движении жидкости или теплоотдачей при свободной конвекции (здесь не рассматривается).

В предыдущей главе были рассмотрены способы теоретического анализа процессов теплоотдачи на основе теории пограничного слоя на примере продольно и понеречно-омываемой пластины и вынужденного движения жидкости в гладкой круглой трубе. При этом физические константы (X., ц, р, С), от которых зависит способность жидкости переносить теплоту, принимались постоянными. Кроме того, не учитывалось влияние свободной конвекции, которая может либо усиливать теплоотдачу при вынужденном движении жидкости, либо ослаблять ее. Однако пока невозможно теоретическое определение теплоотдачи при наружном омывании тел более сложной формы или при вынужденном движении в трубах некруглого сечения с шероховатыми стенками с учетом непостоянства физических констант жидкости и свободной конвекции. Следует отметить, что значительная часть сведений о процессах переноса теплоты, которыми мы располагаем, была получена экспериментально. Поэтому инженерные расчеты теплоотдачи в основном построены на экспериментальных сведениях.

С появлением ЭВМ развиты методы численного решения дифференциальных уравнений, описывающих теплоотдачу (гл. 15). Исследование теплоотдачи методом математического моделирования с решением соответствующих дифференциальных уравнений, можно считать эквивалентным экспериментальному исследованию. Результаты математического моделирования и их решения точны настолько, насколько точно исходные уравнения описывают изучаемое физическое явление.

Сопоставляя аналитический метод с методами математического моделирования и экспериментального исследования физических явлений, следует отдать им предпочтение в указанной последовательности с точки зрения ценности и стоимости полученных результатов.

Экспериментальное исследование требует создания весьма дорогих стендов. Сам эксперимент обычно трудоемкий, требует больших капиталовложений и времени. Поэтому, когда другие методы непригодны, прибегают к экспериментальному исследованию.

Ниже рассмотрены результаты экспериментальных исследований при вынужденной конвекции в трубах.

Начальный участок трубы. Теплоотдача жидкости в трубе зависит от режима ее движения. Режим движения жидкости в трубе ламинарный

при Re < Яекр. i ~ 2000. Число Re^. i — нижнее критическое число Рейнольдса.

Режим движения в трубе развитый турбулентный при Re > Re^, 2 ~ ~10⁴. Режим движения в трубе переходный при Re = 2*10³…2*10⁴. Уже при Re > 2000 после внесения возбуждения в поток в нем не может восстановиться ламинарный режим движения. Если режим движения в трубе ламинарный, то при входе жидкости в трубу на ее стенках образуется ламинарный пограничный слой, который по мере удаления от входа утолщается и на некотором расстоянии от входа заполняет все сечении трубы.

Если режим движения переходный или турбулентный, то при входе жидкости в трубу на ее стенках, так же как и при ламинарном режиме, образуется ламинарный пограничный слой, который на некотором удалении от входа переходит в турбулентный, утолщаясь и заполняя все сечение трубы (рис. 16.10).

Если Re >~ 5−10⁴, то при входе в трубу на ее стенках практически сразу образуется турбулентный пограничный слой.

Путь жидкости от входа в трубу до сечения, в котором пограничный слой сливается с общим потоком, называют длиной гидродинамического начального участка и обозначают /_н. На некотором расстоянии от входа в трубу (координата д:) при х > /" движение называют стабилизированным. Распределение скорости стабилизированного движения не зависит от распределения скорости на входе в трубу (х = 0), но теплообмен может оказать влияние на распределение скорости в любом сечении трубы.

Сразу после входа жидкости в трубу теплообмен происходит только в тонком слое потока (у внутренней поверхности). Ядро потока в этом случае еще не участвует в теплообмене. По мере удаления жидкости от входа в трубу ядро теряет (получает) теплоту и поэтому температура на его периферии уменьшается (увеличивается), а толщина теплового пограничного слоя растет.

Участок, на котором профиль температуры зависит от условий на входе (происходит нарастание пограничного слоя до заполнения попереч;

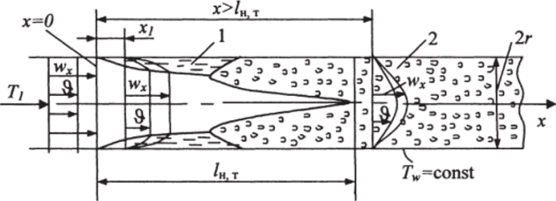
Рис. 16.10. Распределение скорости w_x = /(г) и температуры Э = (Г, -7*_w) = /(г) по длине трубы в сечениях: х = 0, х ^ш х_ь х > х_КТ: 1 — ламинарный пограничный слой; 2 — турбулентный пограничный слой ного сечения трубы), называют тепловым начальным участком и обозначают /", т (рис. 16.10).

На рис. 16.10 представлено распределение скорости w_x и избыточной температуры 0 = Т — T_w по длине трубы при турбулентном режиме движения жидкости.

На некотором расстоянии / от входа в трубу и далее по потоку / > /" _т между жидкостью и стенками происходит стабилизированный теплообмен. Стабилизированным называют конвективный теплообмен в трубе на некотором удалении от входного сечения, где сохраняется определенный закон изменения граничных условий на стенке трубы по ее длине, а поле температуры практически не зависит от характера распределения температуры и скорости в этом сечении. При этом свойства жидкости постоянны для некоторых видов граничных условий на стенке трубы (например, при постоянной температуре стенки или постоянной плотности ее теплового потока); распределение температуры (от стенки) по сечению потока при стабилизированном теплообмене подобно в различных сечениях трубы. Коэффициент теплоотдачи, отнесенный к местному температурному напору, не изменяется по длине трубы.

Если на всей длине начального участка трубы движение остается ламинарным, то от входа в трубу и далее по потоку на длине теплового начального участка локальный а_х и средний, а коэффициенты теплоотдачи уменьшаются, так как на этом участке происходит увеличение толщины ламинарного пограничного слоя.

Если на длине теплового начального участка ламинарный пограничный слой переходит в турбулентный, то наблюдается иной характер изменения коэффициентов теплоотдачи а_х и а.

Длину теплового начального участка /_{н> т} можно определить [23] при ламинарном течении жидкости с постоянными физическими параметрами и температурой на входе при постоянной температуре стенки T_w = const для гидродинамического стабилизированного движения в трубе по формуле (l_{H T}/d)= 0,055Ре; при турбулентном движении /_{н т} = (10…15)*/.

Мак-Адамс [24] получил зависимость для среднего числа Нуссельта при турбулентном движении на начальном участке трубы (при Re у > 1 10⁴ и 0,7<�Ргу <120):

где Nu/ = а//Х; d- диаметр трубы, м (все физические константы, кроме, взяты при средней по длине трубы / температуре tj)

где средние по сечению трубы температуры на входе и на расстоянии / от входа соответственно; Re^ =wd/v — число Рейнольдса; w = У / / - средняя скорость жидкости, м/с; F-объемный расход жидкости, м³/с;/- площадь поперечного сечения трубы, м²; ц_ш — вязкость при средней по длине трубы температуре стенки.

Участок стабилизированного теплообмена (турбулентный режим). Теплоотдача при течении в трубах круглого сечения достаточно хорошо изучена экспериментально, так как этот процесс является наиболее характерным для многих теплообменных устройств. Исследования показали, что число Nu для вынужденной конвекции в трубах зависят от: чисел Рейнольдса и Прандтля; качества внутренней поверхности стенок (шероховатость); изменения свойств теплоносителя (X, р, С) от температуры; изменения плотности жидкости от температуры или давления.

Непостоянство коэффициента вязкости р оказывает влияние не только на свойства переноса (количества движения), но и на интенсивность теплоотдачи. Косвенное влияние на интенсивность теплоотдачи состоит в следующем: температура изменяет вязкость р, а последняя оказывает влияние на распределение скорости. Это обстоятельство приводит к тому, что интенсивность теплоотдачи оказывается зависящей от направления теплового потока.

Пусть тепловой поток направлен от жидкости к внутренней стенке трубы. В этом случае жидкость у поверхности стенки охлаждается, ее вязкость в этой области изменяется, что приводит к изменению толщины пристенного слоя, движущегося с малой скоростью, а следовательно, и к изменению теплоотдачи, так как этот слой представляет собой основное тепловое сопротивление.

Вязкость газов, как правило, уменьшается с понижением температуры, а капельных жидкостей возрастает. Поэтому если тепловой поток направлен от оси трубы к ее внутренней поверхности, то интенсивность теплоотдачи в газах будет увеличиваться, а в жидкостях уменьшаться. Если тепловой поток направлен от внутренней поверхности к оси трубы, то будет наблюдаться обратная картина. Пока не удается аналитически учесть влияние большинства перечисленных факторов на число Нуссельта, поэтому задача решается экспериментально.

Ламинарный режим. При вынужденном ламинарном движении жидкости в трубе на процесс переноса теплоты влияет свободная конвекция. Она оказывает наиболее сильное влияние при следующих условиях: вектор скорости вынужденного движения жидкости в вертикально расположенной трубе направлен вниз; жидкость нагревается, при этом на внутренних поверхностях стенки может возникнуть свободная конвекция, что приведет к турбулизации пристенного слоя и, как следствие, к интенсификации теплоотдачи.

Зависимость для определения среднего коэффициента теплоотдачи при вынужденном ламинарном движении жидкости в трубе, учитывающая влияние свободной конвекции и направление теплового потока, может быть представлена в виде:

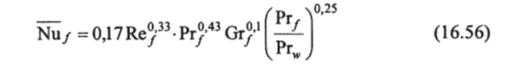
В этом уравнении (16.56) физические константы определяются по средней температуре // (16.55).

Формула (16.55) применима для любой жидкости при — > 50.

а

Для коротких труб (— <50) коэффициент теплоотдачи, полученный d

из (16.56), следует умножить на поправочный коэффициент 8/, значения которого следующие:

Зависимость (16.56) для различных значений числа Грасгофа Gr мо^ жет быть представлена в форме:

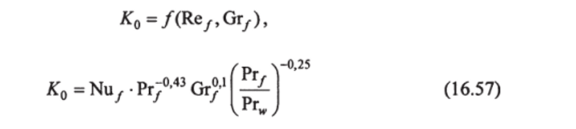
где.

Переходный режим. Между верхней границей области ламинарного и нижней границей турбулентного режима движения в трубах существует область переходного режима. При Re<210³ установится ламинарный режим, при Re>110⁴ — турбулентный. Однако даже при малых числах Рейнольдса режим движения может стать турбулентным на большом рас;

х

стоянии от входа в трубу, например, при — > 500 это происходит уже при.

d

Re<2,610³.

Для переходного режима движения полученные выше формулы применять нельзя. Следует указать на принципиальную неопределенность переходного режима движения жидкости в трубе. Переходной режим движения является неустойчивым, и поэтому он весьма чувствителен к самым разнообразным внешним возмущениям. Теплоотдача в переходной области мало изучена и расчетных зависимостей, дающих удовлетворительные результаты, пока не имеется.

При переходном режиме движения жидкости в трубе (в диапазоне 2 10³ < Re < 10⁴) комплекс Ко (16.57), а следовательно, и число Нуссельта Nu/ резко возрастают; нижний предел комплекса Ко соответствует ламинарному режиму движения жидкости в трубе (К₀ = 0,17 Re®'³³), а верхний — турбулентному (К₀ = 0,021 Re°^{, s}).