Вероятностные задачи с бесконечным числом решений

Встречается много случаев, когда одно и то же решение приходится принимать многократно через регулярные интервалы времени, а сам процесс предполагается бесконечным. При таких условиях часто удобно максимизировать выигрыш на отдельном решении, а не общий выигрыш на бесконечном интервале времени.

Предположим, что имеется некоторый станок, который либо исправно работает, либо полностью выходит из строя. Если станок работает в течение всей недели, то он обеспечивает получение валового дохода в 100 у.е., а если он вышел из строя на этом отрезке времени, то недельный валовой доход равен нулю. Когда станок в начале недели исправлен и профилактически обслуживается, вероятность его выхода из строя в течение этой недели равна 0,4. Если же такого обслуживания нет, эта вероятность составляет 0,7.

Профилактическое обслуживание обходится в 20 у.е. При выходе станка из строя его можно сразу же заменить, что обходится в 120 у.е., или попытаться отремонтировать. Стоимость ремонта составляет 40 у.е., а вероятность получения исправного станка в результате ремонта равна 0,5. При замене всегда получают исправно работающий станок, на котором в течение этой недели будет получен тот же валовой доход 100 у.е. Время, необходимое для ремонта или замены станка, не учитывается. При этих условиях нужно выбрать оптимальную стратегию ремонта и обслуживания.

В этой задаче исходное решение может быть принято при двух различных условиях. Либо станок исправно работает (НО, и в этом случае нужно определить, производить ли профилактику, либо он вышел из строя (В), и тогда нужно определить, заменять его или ремонтировать. Независимо от состояния станка в момент принятия исходного решения и выбора самого решения последующее решение всегда относится к тому же станку, находящемуся либо в состоянии W, либо в состоянии В. На рисунках 8.5а и 8.56 приведены соответствующие «деревья решений».

На рисунках 8.5а и 8.5б, так же как и ранее, квадратики обозначают решения ЛПР, а кружки — решения «природы», т. е. не зависящие от воли ЛПР. На каждой ветви дерева показано, какое решение принято или какова его вероятность, а также прибыль (убыток). За каждым узлом с индексом 2 следует такой же структурный элемент, как за узлом с индексом 1, т. е. процесс принятия решений повторяется неограниченное время по одной и той же логической схеме.

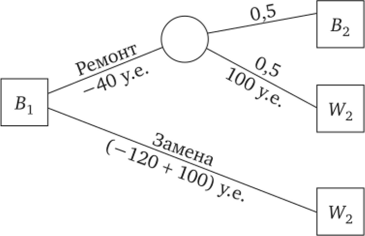
Рис. 8.5а. Принятие решений при начальном условии В.

Рис. 8.56. Принятие решений при начальном условии W.

Предположим, что все будущие доходы (в денежном выражении), следующие за узлом В₂, равны х, а доходы, следующие за узлом W₂, равны у. Если бы значения х и у были известны, то, двигаясь в направлении, обратном течению времени начиная с любого момента, можно было бы определить цены узлов В_} и W) (эффективность решений, принимаемых в этих узлах). Однако поскольку значения х и у не известны, то невозможно даже высказать какие-либо догадки относительно того, какие решения рационально принять в узлах В_г и W_x. Тем не менее разумно предположить^[1], что цены В_г и W₃ будут отличаться от цен В₂ и W₂ на величину выигрыша (прибыли) д, получаемого в течение недельного интервала, разделяющего положение соответствующих узлов во времени. Таким образом, имеем: цена В_г = х + д, цена Wj = у + д. Предположим, что рассматривается узел В, и нужно принять одно из двух решений: ремонтировать станок или заменить его. В случае ремонта и достижения узла W₂ выигрыш равен (100 + у) у.е. При выборе ремонта и попадании в узел В₂ выигрыш составит х у. е. Вероятность достижения любого из этих узлов равна 0,5. Кроме того, необходимо учесть затраты в 40 руб. Таким образом, ожидаемая денежная цена решения о ремонте равна 0,5 (100 +у) + 0,5х — 40 = 0,5х + 0,5у + + 10. Следовательно, решение заменить станок или отремонтировать его определяется тем, какая из величин больше: у — 20 или 0,5х + 0,5у + + 10. Цена этого решения равна х + д.

Таким образом,.

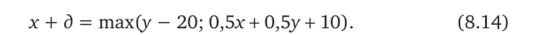
Рассмотрим рисунок 8.56 и, пользуясь такими же рассуждениями, получаем:

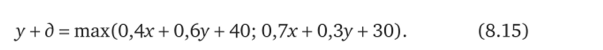
Итак, теперь имеются два уравнения, содержащие три неизвестных х, у и д. Анализ этих уравнений показывает, что если увеличить х х и у на одну и ту же величину, то каждая из максимизируемых величин увеличится также на одну и ту же величину, а следовательно, соотношение между ними не изменится, т. е. решение относительно того, какая из двух величин больше, останется в силе. Отсюда следует, что эти уравнения достаточны лишь для отыскания относительных значений величин х и у и что одной из них можно приписать произвольное значение. Предполагая, что у = 0, получим:

Эту систему уравнений можно решить, пользуясь итеративным алгоритмом. Выберем наугад один из членов, стоящих в правой части, предположив, что он больше другого, и разрешим уравнения относительно х и О. Если —20 > 0,5х + 10 и 0,4х + 40 > 0,7х + 30, то получим:

В результате решения системы (8.18), (8.19) получаем х = -42,9, д — = 22,9. Проверим теперь, достигаются ли при этих значениях искомые максимумы, т. е. выполняются ли принятые предположения. Должны выполняться неравенства:

Таким образом, первое предположение неверно, а второе верно. Повторим расчет, изменив предположение о соотношении величин только первого уравнения. При этом допущении имеем:

Из уравнений (8.20) и (8.21) получаем:

При этом значении х получаем:

Эти неравенства почти точно соответствуют допущениям, принятым при вычислении значений х и д. Можно показать, что эти значения х и д являются единственными решениями уравнений (8.16) и (8.17). Метод отыскивания этих значений ясно показывает, что оптимальная стратегия заключается в выполнении профилактического обслуживания и ремонта вышедшего из строя станка.

Такой ход рассуждений имеет весьма общий характер, и они легко распространяются на случай, когда вводятся более двух видов узлов и в каждом узле имеется более двух альтернатив [1].

Очевидно, что идею построения дерева решений и метод его анализа, начинающегося с последнего во времени решения и проводимого в направлении, обратном течению времени вплоть до исходного решения, можно также применить к детерминированным задачам, в которых решения можно принимать последовательно во времени. Во многих отношениях эти задачи проще, ибо в них отсутствуют узлы, где решения принимаются природой и не фигурируют математические ожидания. Для решения таких задач, как правило, не нужно строить «дерева», хотя ход рассуждений в принципе остается прежним.

Перечислим некоторые из задач, которые можно решать методом динамического программирования: 1) распределение капиталовложений и ресурсов по отраслям промышленности и другим экономическим единицам; 2) определение порядка обработки деталей на нескольких станках для минимизации общего времени обработки; 3) решение транспортных задач; 4) определение размеров ресурсов для минимизации общих издержек; 5) анализ вариантов замены и модернизации оборудования; 6) выбор тематики НИОКР; 7) определение направлений развития промышленных предприятий.

Трудности постановки конкретных задач динамического программирования заключаются в сложности выбора параметров, характеризующих состояние системы и распределение процесса на этапы (шаги).

Кроме того, необходимым условием применения метода динамического программирования является аддитивность эффективностей всех решений, а также независимость будущих результатов от предыстории того или иного состояния.

• [1] Здесь принимается предположение, что различие цен Вi и В2 равно различию ценWj и W2. Это предположение оправдано при условии, когда за В2 и W2 следует большоечисло решений. Именно такой процесс рассматривается в данном случае.