Двухэлементные цени. 
Электротехника и электроника

Рассмотрим особенности использования классического метода при анализе /?С-цспи (рис. 1, я). Для се описания воспользуемся топологическим и компонентными уравнениями.

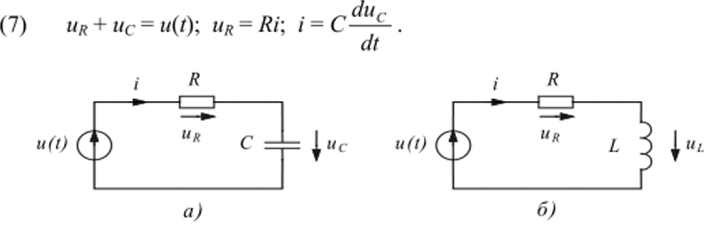
Рис. 1. Двухэлементные RC- и Л?-цепи Используя (7), получаем дифференциальное уравнение первого порядка.

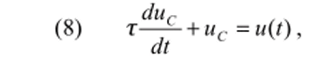
где т = RC — постоянная времени. Как будет показано ниже, постоянная времени является одним из основных параметров двухэлементных цепей.

Временной анализ цепи на рис. , а сводится к решению уравнения (8). По известному напряжению и_с на конденсаторе с помощью компонентных уравнений (7) определяется ток / в цепи и напряжение u_R на резисторе.

Общее решение уравнения (8) будем искать в виде ис,_с ⁼ U exp (pi). Подстановка U exp {pi) в (8) приводит к характеристическому уравнению.

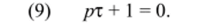
Из уравнения (9) находим р = -1/т. Таким образом, общее решение уравнения (8) имеет вид.

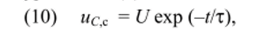
где U — постоянная интегрирования, определяемая из начальных условий (при / = 0).

Для нахождения частного и полного решения уравнения (8) рассмотрим несколько конкретных видов воздействия «(/), которое прикладывается к /?С-цепи в момент времени / = 0.

1.Постоянное напряжение: u (t) = Е (/ > 0). Из (8) следует, что частное решение имеет вид и_Сл = ?, так как в установившемся режиме iduc/dt = 0. Поэтому полное решение уравнения (8) для этого случая с учетом (10) выражается соотношением.

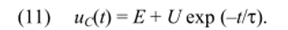
Полагаем, что напряжение (11) при / = 0 равно Uq, тогда U = U₀ — Е, и полное решение принимает вид.

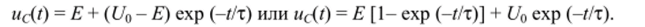
Форма напряжения udt) на емкости для различных начальных условий (Uo) приведена на рис. 2,а, б, в.

Рассмотрим весьма важный в практическом отношении случай нулевых начальных условий (Uo = 0), для которого.

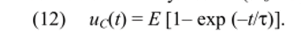
С помощью выражения (12) можно определить длительность переходного процесса как время Г_га" за которое напряжение на емкости увеличивается от 0 до 0,9 Е. Из уравнения Е-Е exp (—Z'nr/r) = 0,9 Е находим Т_т = 2,3 т.

Для области малых времен (при t —" 0) экспоненту в (12) можно представить первыми двумя членами степенного ряда (Тейлора), т. е. exp (-t/z) * = 1 — t/z. Поэтому для этого случая напряжение на конденсаторе изменяется по линейному закону udt) ~ Et/z. Такой закон соответствует изменению напряжения на выходе идеального интегратора. Действительно, для воздействующего на цепь напряжения u (t) = ?, получаем u (t) dt = Е dt = = Et. В идеальном интеграторе величина т определяет время, за которое напряжение на емкости изменяется от 0 до Е. Для рассматриваемой цепи при t = z имеем udi) = Е — Е схр (-1) = 0,63 Е (рис. 2, я). Следовательно, в том случае, когда напряжение снимется с емкости С, цепь на рис. 1// для области малых времен (t" z) выполняют операцию интегрирования.

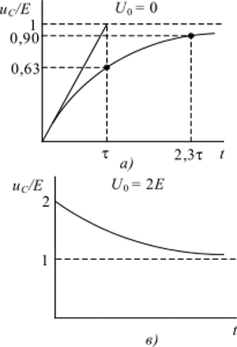
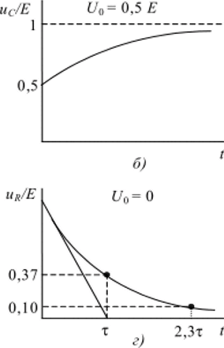
Рис. 2. Временные зависимости напряжения на элементах /?С-цепи:

udO при начальных напряжениях на конденсаторе ?/₀ = 0 (a), Uo = 0,5Е (б),

Uq = 1,5Е (в); U/i (t) при начальном напряжении на конденсаторе С/₀ = 0 (г) Используя (12), найдем напряжение на сопротивлении R при нулевых начальных условиях.

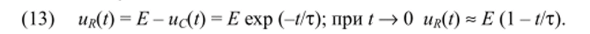
Графические зависимости u_R(t)/E, построенные с помощью (13), приведены на рис. 2, г. Для этого случая время переходного процесса Т_пп определяется как интервал времени, за который происходит уменьшение напряжения u_R(t) на сопротивлении R от Е до 0,1 Е.

2. Экспоненциальное воздействие: u (t) = Е схр (а/), где, а = const. Из (8) следует, что в этом случае вынужденная составляющая ис.в (0 должна также изменяться по экспоненциальному закону. Подстановка и с, _в(0 ⁼ В exp (at) в (8) приводит к характеристическому уравнению атВ + В = Е, откуда находим В = Е/( 1 + ат). Поэтому полное решение для этого случая с учетом (10) имеет вид.

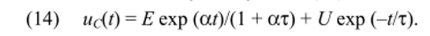
Для начальных условий Мс (0) = U₀ из (14) находим U = U₀ — Е/( 1 + ат). С учетом этого решение (14) принимает вид (а Ф -т).

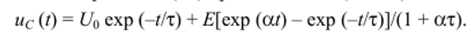
Для, а = т вынужденная составляющая имеет вид Et exp (а/). Используя (10), находим полное решение для этого случая.

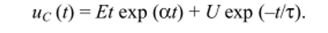
• 100
• 3. Гармоническое воздействие: u (t) = Е cos (tot + а). Для этого случая частное решение можно найти методом комплексных амплитуд. Однако будем искать ег о как решение уравнения (8) в виде

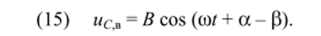
Подстановка (15) в (8) дает уравнение.

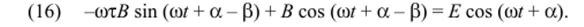
Для нахождения В и Р преобразуем (16) к виду.

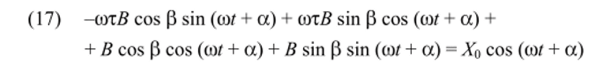
и, приравняв коэффициенты при sin (tot + а) и cos (со/ + а) левой и правой частей (17), получим систему из двух уравнений.

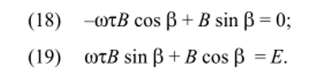
Из (18) определяем.

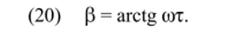
Используя (19), (20) и известные соотношения 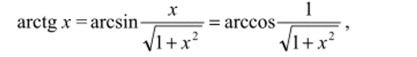находим.

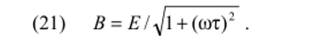
Используя (10), (15), (20), (21), запишем полное решение.

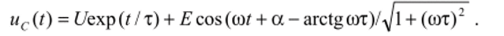
Полагаем, что напряжение u^t) при / = 0 равно ?/₀, тогда.

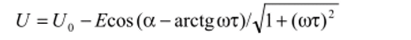
и полное решение уравнения (8) принимает вид.

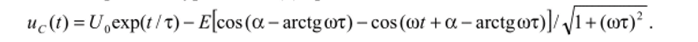
Отмстим, что рассмотренными видами воздействия, по сути дела, и ограничивается представление решения уравнения (8) в аналитической форме.