Канонические формы уравнения и модальное управление

Ввиду того что существует множество эквивалентных форм представлений уравнений состояний, можно выбрать из них наиболее удобное для использования в данном конкретном случае. Такие формы уравнений называют каноническими [4]. Поскольку возможно много различных приложений, используется несколько канонических форм. Здесь рассмотрим преобразование уравнений состояний в каноническую форму, называемую управляемой формой Луенбергера.

Уравнение состояния вида.

называется управляемой формой Луенбергера |4|. Характеристическое уравнение матрицы А этого уравнения имеет вид.

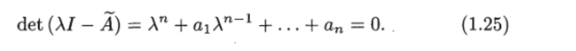
Коэффициентами характеристического уравнения являются элементы последней строки матрицы А уравнения (1.24) с противоположным знаком.

Теорема 1.1. Для того чтобы уравнение состояния

неособым преобразованием можно было преобразовать в управляемую форму Луенбергера (1.24), необходимо и достаточно, чтобы пара (А, В) была вполне управляема.

Доказательство. Необходимость следует из того, что управляемая система, описываемая уравнением (1.24), является вполне управляемой (см. доказательство утверждения 1.2) и свойство управляемости не меняется при неособом преобразовании.

Докажем достаточность, т. е. покажем, что существует неособое преобразование х = Tz, при котором исходное уравнение преобразуется к виду (124), где.

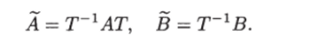
Так как пара (>4, В) вполне управляема, то матрица управляемости является неособой. Поэтому линейное алгебраическое уравнение.

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

Рассмотрим матрицу

где h является неизвестным n-вектором, имеет решение. Подставив в последнее уравнение выражение для матрицы управляемости, получим или Эта матрица является неособой в силу того, что матрица.

является неособой. Последнее следует из того, что, так как в силу равенств (1.27) все элементы на неглавной диагонали последней матрицы равны единице, а над ней равны нулю, det R = 1 или det R = —1.

Искомым преобразованием является преобразование.

или Действительно, дифференцируя последние равенства по времени и подставляя выражение для производной х из (1.26), получим.

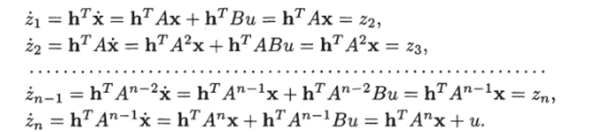
Подставляя в последнее равенство выражение для А^п из соотношения 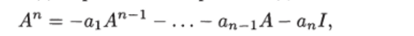которое получается из теоремы Кэли-Гамильтона, находим 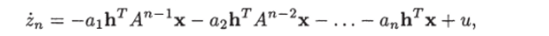или, учитывая (1.286),.

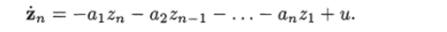
Таким образом, исходное уравнение преобразуется в управляемую форму Луенбергера при помощи преобразования (1.28).

При неособом преобразовании характеристические уравнения исходной системы (1.26) и преобразованной системы (1.24), т. е. det (A/ - А) = 0 и det (A7 — А) = 0, совпадают (см. § 1.4.5).

Пример 1.6. Преобразовать уравнение состояния.

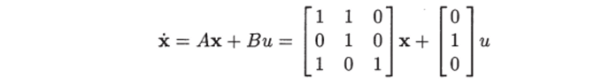
в управляемую форму Луенбергера.

Решение. Произведения ЛВ, А²В и матрица управляемости имеют вид.

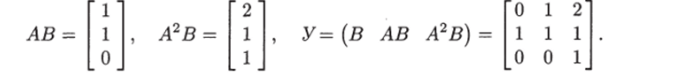
Так как det У = — 1, то пара (А, В) вполне управляема. Следовательно, данное уравнение может быть преобразовано в управляемую форму Луепбергера. Характеристические уравнения матриц А и А совпадают и имеют вид.

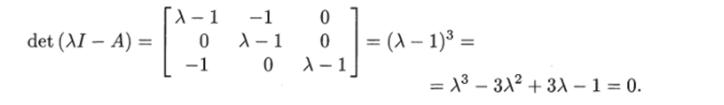
Поэтому элементами последней строки матрицы А будут и преобразованное уравнение имеет вид.

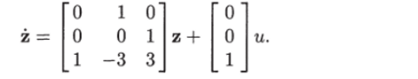
Модальное управление — если линейный стационарный объект вполне управляем, то существует такой линейный закон управления, при котором корни характеристического уравнения замкнутой системы равны наперед заданным числам. Способ управления, основанный на размещении корней характеристического уравнения определенным образом, называют модальным управлением [55].

Теорема 1.2. Пусть заданы линейный стационарный объект

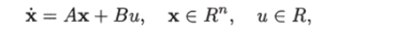
I (/ ^ п/2) пар произвольных комплексно-сопряженных чисел А* = = Qfj ± j (3i (t = 1,2,…,/) и п — 21 произвольных действительных чисел X_s = a_a (s = 2/ + 1,…, n).

Если данный объект вполне управляем, то существует закон управления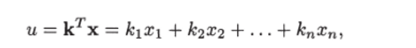

при котором корни характеристического уравнения замкнутой системы равны заданным числам.

Доказательство. Рассмотрим преобразование x = Tz, которое преобразует уравнение объекта в управляемую форму Луенбергера (1.24). Характеристическое уравнение объекта имеет вид (см. (1.25))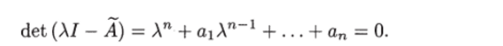

Чтобы корни характеристического уравнения замкнутой системы были равны заданным числам, оно должно иметь вид.

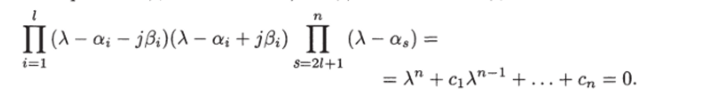
Искомый закон управления найдем, если подставить выражение z = = Т^_1х в формулу (1.29):

или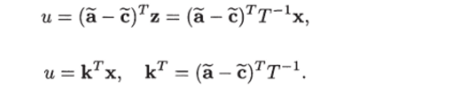

Теорема, аналогичная теореме 1.2, справедлива и в случае векторного управления [4, 55]. Сформулируем ее без доказательства.

Теорема 1.2а. Пусть заданы линейный стационарный объект

I (I ^ п/2) пар произвольных комплексно-сопряженных чисел А* = = orj ± jfii (г = 1,2,…,/) и п — 21 произвольных действительных чисел As = ос₉ (з = 21 + 1,…, п).

Если данный объект вполне управляем, то существует закон управления и = Кх (К — (г х п)-матрица), при котором корни характеристического уравнения замкнутой системы равны заданным числам.

Утверждение 1.3. Пусть характеристическое уравнение одномерной управляемой системы (1.26) имеет вид

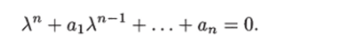
Для того чтобы характеристическое уравнение замкнутой системы имело вид .

нужно выбрать закон управления вида

Характеристическое уравнение замкнутой системы будет иметь такой вид, если принять закон управления.

Действительно, подставив этот закон управления в уравнение (1.24), получим.

где.

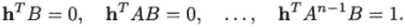
а векторная переменная h^T в последней матрице определяется из уравнений.

Это утверждение непосредственно вытекает из доказательств теорем 1.1 и 1.2.

Пример 1.7. Управляемая система описывается уравнением.

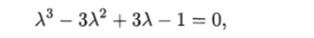
Определить закон управления, при котором корни характеристического уравнения замкнутой системы равны Ai_t2 = — 1 ± 3j, A3 = -1.

Решение. Согласно утверждению 1.3, чтобы найти требуемый закон управления, нужно знать коэффициенты характеристических уравнений управляемой и замкнутой систем, а также обратную матрицу преобразования уравнений управляемой системы в управляемую форму Луенбергера. Характеристическое уравнение управляемой системы имеет вид (см. пример 1.4).

а характеристическое уравнение замкнутой системы — вид В принятых выше обозначениях и соответственно.

Чтобы определить матрицу Т~^г, нужно сначала составить и решить систему уравнений

Входящие в эти уравнения матрицы имеют вид.

Поэтому указанные выше уравнения принимают вид.

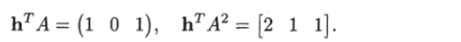
Отсюда получаем h^r = (О 0 1). Произведения h^тА и h^тА² имеют вид

Поэтому для матрицы Т~¹ получаем соотношение.

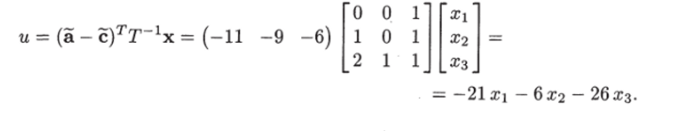
а искомый закон управления принимает вид.