Основные методы вычисления определенных интегралов

Поскольку формула Ньютона — Лейбница позволяет свести вычисление определенного интеграла к вычислению любой его первообразной с последующей двойной подстановкой нижнего и верхнего пределов, то определенные интегралы вычисляются на практике теми же методами, что и неопределенные.

Перечислим три основных подхода к интегрированию^[1]:

• 1) использование алгебраических, тригонометрических и прочих преобразований подынтегральной функции, а также свойств интегралов;
• 2) замена переменной интегрирования;
• 3) интегрирование по частям.

В результате применения этих методов интеграл последовательно упрощается и в итоге сводится к вычислению одного или нескольких табличных интегралов (или уже известных интегралов).

Несколько слов об интегрировании разрывных функций. Выше, в гл. 1, было доказано, что если функция / определена и ограничена на отрезке [а,?>, причем имеет на нем конечное число точек разрыва, то функция / интегрируема по Риману на указанном отрезке. Рассмотрим два основных подхода к вычислению на практике интегралов от таких функций.

Если по разные стороны от точек своего разрыва подынтегральная функция имеет различные аналитические представления, то, пользуясь свойством аддитивности определенного интеграла, разбивают его на сумму интегралов (точки разбиения промежутка интегрирования совпадают с точками разрыва подынтегральной функции), а затем каждый из полученных интегралов, доопределив подынтегральную функцию до непрерывной и вычислив первообразную, вычисляют при помощи стандартной формулы Ньютона — Лейбница.

Если же на всем промежутке интегрирования (исключая точки разрыва) функция задается одной и той же формулой, то первообразная также будет иметь один вид (с точностью до константы), и в этом случае для вычисления определенного интеграла вначале методами, приемлемыми для неопределенных интегралов, находят для функции/одну какую-либо первообразную (непрерывную между соседними точками разрыва /); затем вычисляют обобщенную первообразную (непрерывную на всем отрезке [а, Ь] функцию F, такую что F'(x) = f (x) всюду на [а, Ъ], за исключением, возможно, точек разрыва) и после этого применяют формулу Ньютона — Лейбница.

Отметим, что в последнем случае возможным является вычисление определенного интеграла без нахождения обобщенной первообразной. Приведем в связи с этим следующую теорему, имеющую важное теоретическое значение для понимания процедуры вычисления широкого класса определенных интегралов от разрывных функций.

Теорема 3.1 (формула Ньютона — Лейбница для ограниченных функций, имеющих на отрезке интегрирования конечное число точек разрыва). Пусть функция/собственно интегрируема на отрезке [а, Ь] и F — такая функция, что F'(x) = f (x) всюду на [а, Ь], за исключением, быть может, конечного числа внутренних точек с, (? = 1,2,…, р) и концов отрезка, а и Ь, где функция F терпит разрывы первого рода'¹. Тогда справедлива формула

Доказательство. Рассмотрим непрерывную на каждом из отрезков [^ci.c_i+i] функцию.

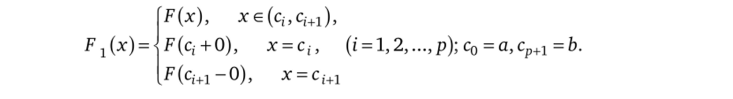
Возьмем теперь произвольное разбиение Т:а = х₀<�х₁<…<�х_п=Ь отрезка [а, Ь], такое чтобы точки q, i = l, 2,…, р, входили в число точек разбиения. Тогда, с одной стороны,.

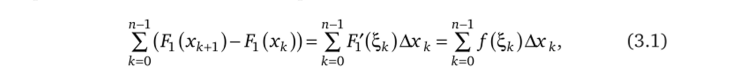
где Z, k^s(^xk>^xk+i) (^по теореме Лагранжа о конечных приращениях). С другой стороны,.

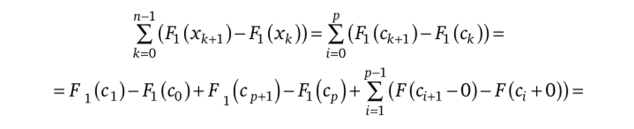
¹ Функция F не является первообразной для функции/на [а, Ь].

Переходя к пределу, устремив диаметр разбиения А_т к нулю, из формулы (3.1) получаем.

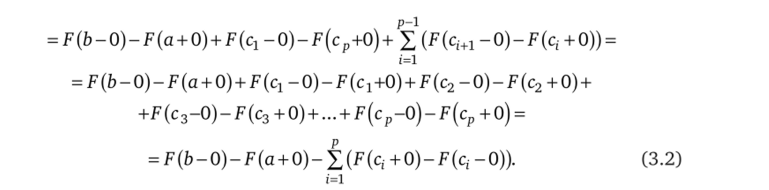
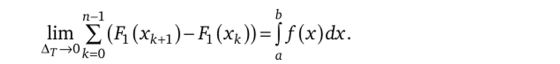
Сопоставляя полученный результат с формулой (3.2), приходим к выводу, что.

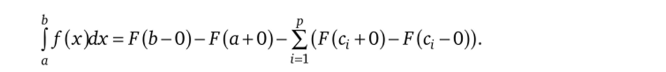
Теорема доказана.

Замечание 3.1. Разность F (с_|+1 + 0) — F (с, — 0) есть величина скачка значений функции F в точках разрыва.

Итак, рассмотрим способы аналитического вычисления определенных интегралов, основанные на использовании формулы Ньютона — Лейбница.

• [1] Вычисление определенного интеграла как предела интегральной суммы было рассмотрено в гл. 1.