Закон сохранения момента импульса

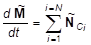
Если сумма моментов внешних сил, действующих на систему материальных точек, относительно точки О, равна нулю, то как следует из уравнения (22.2), для такой системы. Это означает, что в случае момент импульса системы материальных точек остается постоянным:

M_O = const. (23.1).

Этот результат составляет содержание закона сохранения момента импульса.

В общем случае внешние силы являются суммой внешних сил взаимодействия и сил инерции.

Если в инерциальной системе отсчета (силы инерции равны нулю) рассматривать движение замкнутой системы тел (внешние силы взаимодействия равны нулю), то относительно любой неподвижной точки момент импульса такой системы не изменяется с течением времени.

Закон сохранения момент импульса относительно некоторой точки можно применять и к незамкнутой системе тел, если сумма моментов внешних сил относительно этой же точки будет равна нулю.

Момент импульса твердого тела. Понятие тензоре инерции. Главные оси инерции

В § 19 мы выяснили, что при движении тела под действием произвольно приложенных сил все его точки имеют разные кинематические параметры. Но движение одной точки тела, а именно, центра инерции, мы можем описать сразу с помощью уравнения (19.3).

Если теперь можно было бы описать вращение тела вокруг центра инерции, то задачу можно было бы считать выполненной.

Таким образом, нам нужно решить уравнение моментов (22.2), записанное в Ц-системе с неподвижным началом в центре инерции С:

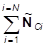
. (24.1).

В этом уравнении:

— собственный момент импульса тела;

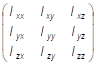
— сумма всех моментов сил (включая моменты центробежных сил инерции), записанных относительно точки центра масс С.

Для решения этого уравнения необходимо определить направления осей координат, проведенных из центра инерции.

И тут возможны, по крайней мере, два варианта.

• а) Оси декартовой системы координат Ц-системы не изменяют своего направления в инерциальной системе отсчета, т. е. Ц-система движется в инерциальной системе отсчета поступательно. В этом случае сумма моментов всех сил инерции равна нулю, так как в такой системе возникают только поступательные силы инерции, момент которых равен нулю (20.6). Следовательно, в этом случае мы можем рассчитывать вращательное движение тела вокруг центра инерции, не учитывая, как он движется, т. е. считать его неподвижным. Момент импульса тела в такой Ц-системе, который всегда равен собственному моменту импульса тела, часто называют спином (от англ. spin — верчение).
• б) Оси декартовой системы координат Ц-системы жестко связаны с самим телом и, следовательно, могут вращаться вместе с телом в инерциальной системе координат. В этом случае момент импульса тела всегда равен нулю, и, следовательно, сумма моментов всех сил всегда равна нулю (тело в такой системе отсчета покоится), но при этом придется учитывать моменты центробежных сил инерции.

Несмотря на внешнюю простоту уравнения (24.1) решение его в общем виде представляет собой весьма громоздкую задачу. Мы постараемся по возможности упростить условия для его решения.

Поскольку дальнейшее рассмотрение движения тела в этом параграфе мы будем связывать только с Ц-системой, для упрощения не будем ставить знак над буквами.

Напишем выражение для момента импульса тела, вращающегося вокруг неподвижной точки С.

Для этого найдем компоненты момента импульса i-ой точки тела, вращающегося вокруг неподвижной точки С с угловой скоростью .

. (24.2).

Здесь мы использовали формулу для вычисления двойного векторного произведения: abc = b (ac) — c (ab).

Тогда x -ая компонента момента импульса М_ix будет равна:

M_ix= _xm_i() — m_ix_i(x_ix+ y_iy+ z_iz) = _xm_i() — m_ix_iy_iy — m_ix_iz_iz.

Аналогично можно получить выражения для остальных компонент момента импульса:

M_iy =_ym_i() — m_iy_iz_iz — m_i y_ix_ix;

M_iz =_zm_i() — m_iz_ix_ix — m_iz_iy_iy.

Просуммировав моменты импульса всех точек тела, получаем выражения для компонент момента импульса тела, вращающегося вокруг неподвижной точки О с угловой скоростью .

M_x = m_i()_x — m_ix_iy_iy— m_ix_iz_iz = I_xxx + I_xyy + I_xzz;

M_y = -m_i y_ix_ix + m_i()_y —m_iy_iz_iz= I_yxx + I_yyy + I_yzz; (24.3).

M_z = -m_iz_ix_ix— m_iz_iy_iy + m_i()_z = I_zxx + I_zyy + I_zzz.

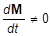
Совокупность величин называется тензором инерции.

Из уравнений (24.3) видно, что в общем случае направление вектора момента импульса тела М может не совпадать с направлением вектора угловой скорости .

Например, пусть вектор угловой скорости направлен вдоль оси Z (= _ze_z). Это означает, что компоненты вектора _x и _y равны нулю, а из (24.3) следует, что М_x= -m_ix_iz_iz, а М_y = -m_iy_iz_iz.

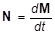
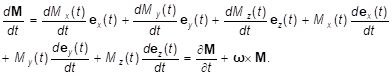
Следовательно, при вращении тела вокруг неподвижной оси момент импульса может менять свое направление, и, следовательно,. Отсюда следует, что для поддержания вращения тела даже с постоянной угловой скоростью в общем случае необходимо приложить некоторый момент сил .

В общем случае все элементы тензора отличны от нуля. Однако оси координат можно выбрать таким образом, чтобы все недиагональные элементы тензора I_ik, которые называются центробежными моментами инерции, обратились в нуль. При такой ситуации говорят, что оси тела, совпадающие с осями координат, являются главными осями инерции. В этом случае величины I_xx= I_x, I_yy= I_y, I_zz= I_z называют главными моментами инерции относительно соответствующих осей, вычисление которых сводится к вычислению следующих сумм:

I_x = m_i(); I_y =m_i(); I_z =m_i(). (24.4).

Таким образом, если оси координат Ц-системы направлены вдоль главных осей инерции тела, то центробежные моменты инерции отсутствуют. В этом случае при вращении тела вокруг главной оси сумма моментов центробежных сил инерции также равна нулю.

Можно показать, что через любую точки тела можно провести три взаимно перпендикулярные главные оси, а если они проведены через центр инерции, то они называются центральными главными осями.

В однородном твердом теле правильной формы центральные главные оси совпадают с осями симметрии этого тела. Если в Ц-системе выбрать оси координат таким образом, чтобы они совпали с центральными главными осями тела, то этом случае собственный момент импульса тела примет вид:

М = I_x(t) e_{x(t) + Iy(t) ey(t) + Iz(t) ez(t). (24.5)}

В этом случае направление вектора момента импульса тела М уже совпадает с направлением вектора угловой скорости .

Например, пусть угловая скорость совпадает с центральной главной осью Z. Тогда из (24.5) следует, что М = I_z.

Таким образом, если = const, то М = const, и суммарный момент внешних сил равен нулю (N_{внеш. сил} = 0).

Поэтому вращение вокруг центральных главных осей называют вращением вокруг свободных осей, так как для поддержания такого движении не требуется момента внешних сил.

При свободном вращении в силу случайных факторов может произойти некоторое отклонение направления вектора угловой скорости, и тогда появляются моменты центробежных сил инерции, которые либо стремятся вернуть ось вращения в исходное положение, либо уводят еще дальше ось вращения от первоначального расположения. В первом случае это будет устойчивое вращение, а во втором нет. Если тело вращается в условиях, когда момент внешних сил относительно оси вращения равен нулю, то устойчивым оказывается только вращение вокруг центральных главных осей, соответствующих максимальному или минимальному значениям моментов инерции. Вращение вокруг главной оси со средним моментом инерции неустойчиво. В этом Вы можете убедиться сами, подбрасывая щелчком с края стола, например, коробок спичек.

Если суммарный момент всех сил, действующих на тело, не равен нулю, то для описания его движения нужно воспользоваться уравнением моментов (22.2). Направления осей координат должны совпадать с главными осями инерции, и при взятии производной от момента импульса тела мы должны учесть, что орты координатных осей Ц-системы меняют свое положение и, следовательно, их производные по времени отличны от нуля.

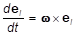
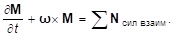
Мы учли, что, где — угловая скорость вращения тела.

Итак, окончательно уравнение моментов для тела относительно центра инерции, будет иметь вид:

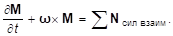
(24.6).

Проекции этого уравнения на координатные оси называются уравнениями Эйлера, которые и позволяют в принципе всегда определить движение тела.

На этом мы закончим обзор общего случая движения твердого тела.

Расчетные соотношения для описания вращения тела можно получить, перейдя к рассмотрению частного случая — вращение тела вокруг неподвижной оси. Это, хотя и частный, но очень распространенный и практически важный случай.