Неравенство Чебышева и закон больших чисел

Теорема Чебышева. Пусть случайная величина Y > 0 и ее математическое ожидание MY существуют. Тогда для любого в > 0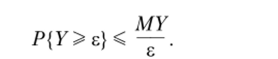

Доказательство проводим для дискретной случайной величины.

• 4.3. Неравенство Чебышева и закон больших чисел
• 123

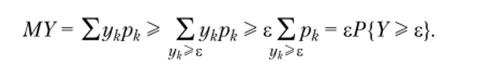
Разделив теперь обе части на в, получим искомое неравенство.

Следствие. Пусть случайная величинах имеет математическое ожидание Мх и дисперсию Dx. Тогда имеет место неравенство (которое чаще называется неравенством Чебышева)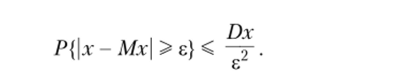

Доказательство. Обозначая Y = (х — Мх)² > 0 и применяя к Y лемму, получаем.

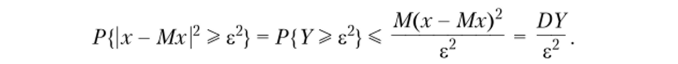
Неравенство Чебышева имеет принципиальное значение: оно позволяет оценивать вероятности отклонения значений случайной величины от среднего значения только с помощью дисперсии; оно дает хотя и очень грубую, но гарантированную оценку.

Пример 4.8. Рассмотрим случайную величину S" — число гербов при п бросаниях симметричной монеты. Математическое ожидание S_n равно пр_} а дисперсия равна пр ( 1 — р). Вычисляя эти характеристики распределения при данных значениях параметров п = 100 и р = ½, используя неравенство Чебышева, получим.

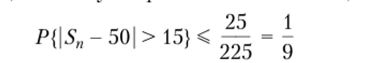
(ср. с вычисленным по таблицам биномиального распределения точным значением этой вероятности P{S" - пр > 15} = 0,178).

Неравенство Чебышева весьма полезно при выводе так называемого закона больших чисел.

Закон больших чисел. Законом больших чисел называется, по предложению А. А. Маркова, целая группа теорем, изучающая поведение средних арифметических случайных величин. Содержание закона больших чисел, грубо говоря, в том, что арифметическое среднее очень большого числа случайных величин почти постоянно.

Теорема Бернулли. Пусть последовательность {х^} соответствует схеме испытаний Бернулли: х, … х_п независимы и P{x_k = 1} = р, Р{х_к = 0} = q.

Пусть S_n = Х + … + х_п. Тогда для любого г > 0 при п —? °°.

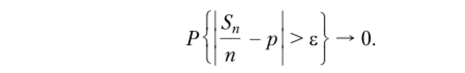
Отношение SJn есть не что иное, как частота событий {х* =1}, происходящего в каждом отдельном испытании с вероятностью Р. Данное неравенство показывает смысл утверждения о том, что частота с увеличением числа испытаний стремится к вероятности.

Теорема Пуассона (обобщение теоремы Бернулли). Пусть последовательность случайных величин {х*, k = 1,…} соответствует схеме испытаний Пуассона: Х|, …, х" независимы и имеют распределение Р{х* = 1} = Р*, Р{х* = 0} = 1 — Р*.

п

Пусть S_n = Х-т*- Тогда для любого? > 0 при я -*? °°.

k= 1.

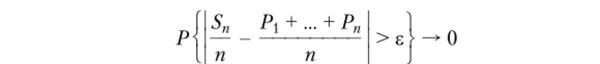
(свою теорему, полученную из варианта центральной предельной теоремы, Пуассон назвал «законом больших чисел»).

Оказалось, что результаты, полученные Бернулли и Пуассоном, являются частными случаями общего закона, который справедлив в более общей ситуации. Это было обнаружено П. Л. Чебышевым.

Определение. Говорят, что последовательность случайных величин х* с математическими ожиданиями Mr* удовлетворяет закону больших чисел, если для любого? > 0 при п —? оо.

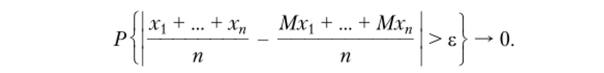
Теорема Чебышева. Пусть случайные величины x_h …, х_п независимы и существуют математические ожидания Mr* и дисперсии Дх*. Для выполнения закона больших чисел достаточно, чтобы существовала постоянная С, чтобы Дх* < С.

Очевидно, что достаточным условиям теоремы Чебышева удовлетворяют случайные величины, рассматриваемые в теоремах Бернулли и Пуассона.

Доказательство. Здесь используется неравенство Чебышева и свойство дисперсий для независимых случайных величин. ВыХ + … + х"

пишем для случайной величины х --неравенство Чебышева ^п

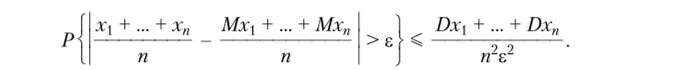
Правая часть неравенства в силу того, что Ох_п < С, не превос- пС С

ходит величины «» = —т., которая стремится к 0 при п —¹• оо, ес- пе пе

ли С и е фиксированы.

Замечание 4.4. В доказательстве теоремы на самом деле используется не взаимная независимость, а некоррелированность случайных величин.

Замечание 4.5. Закон больших чисел не выполняется, например, для величин, имеющих распределение Коши с плотностью Р (х) = -тг. Можно показать, что арифметиче;

я (1 + X)

ское среднее случайных величин x_it… х_п с распределением Коши имеет то же самое распределение, что и каждая величина Х/< и ни к какой постоянной не стремится. Причина такого положения в бесконечности математического ожидания и дисперсии с распределением Коши.