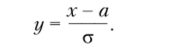Дисперсия. 
Теория вероятностей и математическая статистика

Следующими важными числовыми характеристиками случайной величины, характеризующими меру рассеивания ее значений относительно математического ожидания, является дисперсия и среднеквадратическое отклонение.

Дисперсией Dt, случайной величины ?, называется число.

если математическое ожидание в правой части равенства (3.13) существует.

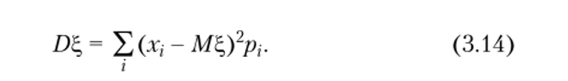
Из (3.13) следует, что в случае дискретной случайной величины Для дисперсии непрерывной случайной величины получаем следующее выражение:

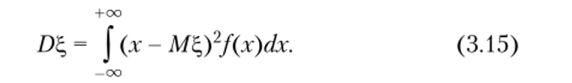
Дисперсия случайной величины обладает следующими свойствами.

Свойство 3.6. Для любой случайной величины D?, > 0. Если с — постоянная, то Dc = 0 и.

Доказательство. То, что D^> 0 для любой случайной величины следует из определения дисперсии (см. (3.14) и (3.15)).

Покажем, что Dc = 0. По свойству Мс = с, поэтому.

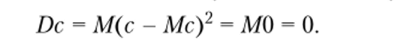
Докажем теперь (3.16). Па основании свойств математического ожидания.

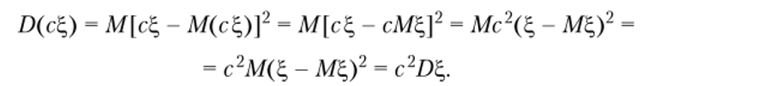
Свойство 3.7. D (%) = Щ² - (Щ)².

Доказательство. Па основании свойств математического ожидания имеем.

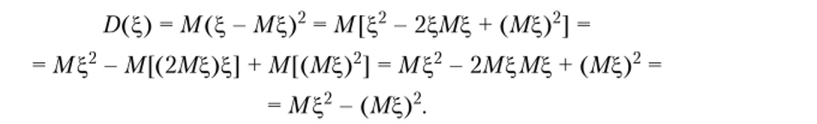
Свойство 3.8. Если случайные величины ^ и ?₂ независимы, то.

Доказательство. По определению дисперсии (3.13) и свойств 3.2 и 3.4 математического ожидания.

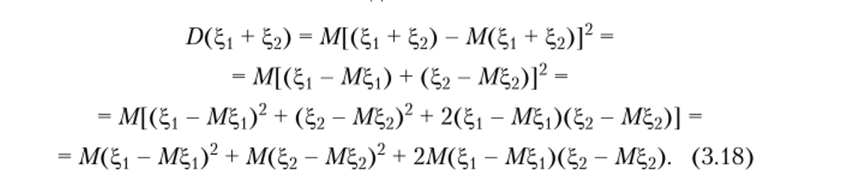
Так как случайные величины ^ и %₂ независимы, то независимы и случайные величины ^ - М% и Е,₂ ~ М^₂> поэтому по свойству Так как дисперсия, как это следует из определения (3.13), имеет размерность квадрата случайной величины, то желательно иметь другую характеристику, характеризующую рассеивание возможных значений случайной величины относительно математического ожидания. Такой характеристикой является УЩ. Величина л1Щ называется среднеквадратическим отклонением.

Наряду с математическим ожиданием и дисперсией используются моменты более высоких порядков.

Величины щ = Щ^к и ц* = М (% - М^)^к называют моментом порядка k и центральным моментом порядка к. Очевидно, что оц и р₂ являются соответственно математическим ожиданием и дисперсией случайной величины Из (3.7) и (3.8) следует, что.

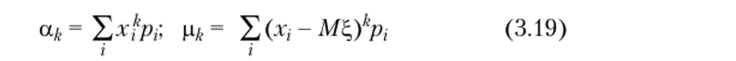
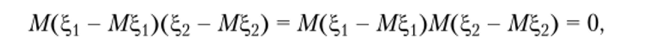
следовательно, из (3.18) следует, что.

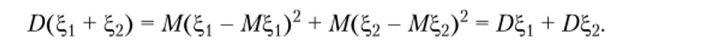
Аналогично можно показать, что справедливо следующее.

Свойство 3.9. Если случайные величины — > ?>_п попарно независимы, то.

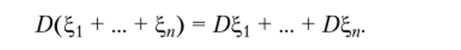
для дискретной случайной величины и.

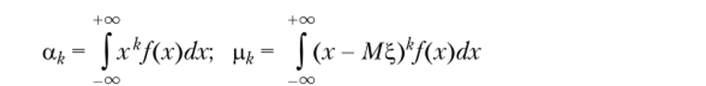
для непрерывной случайной величины.

Третий центральный момент р₃ является характеристикой асимметрии («скошенности») распределения. Поскольку он зависит от единиц, в которых измеряется случайная величина, то обычно рассматривают безразмерную величину.

которая называется коэффициентом асимметрии.

Легко видеть, что если случайная величина ?, распределена симметрично относительно своего математического ожидания, то р₃ = 0. В зависимости от знака 0 кривая распределения имеет положительную или отрицательную асимметрию. На рис. 3.1 изображены кривые распределения, имеющие положительную асимметрию. Соответственно на рис. 3.2 изображены кривые, имеющие отрицательную асимметрию.

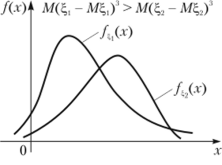
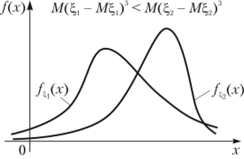
Рис. 3.1 Рис. 3.2

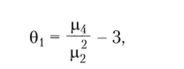
Четвертый центральный момент р₄ является характеристикой островершинности или плосковерпшнности распределения. Обычно рассматривают безразмерную характеристику которая называется эксцессом распределения.

Если 0) > 0, то кривая распределения имеет более высокую и крутую вершину по сравнению с кривой нормального распределения. Если же 0) < 0, то кривая распределения имеет более низкую пологую вершину по сравнению с кривой нормального распределения (рис. 3.3) (предполагается, что обе кривые имеют одинаковые математические ожидания и дисперсии). Отметим, что для нормального распределения 0! = 0.

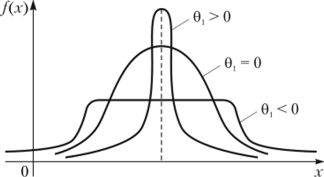
Рис. 3.3.

Пример 3.1. Найдем математическое ожидание и дисперсию биномиально распределенной случайной величины с. По определению математического ожидания.

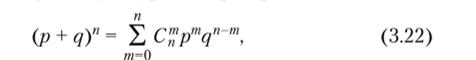aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">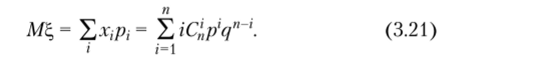

Для вычисления суммы (3.21) рассмотрим равенство откуда, дифференцируя обе части по р и умножая на р, получаем.

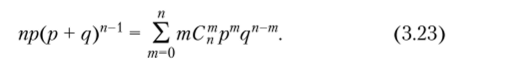
Так как р + q = 1, то из (3.21) и (3.23) окончательно получим Согласно свойству 3.7.

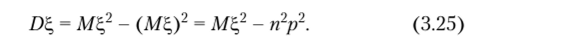
П.

Для вычисления Mt² =? №C"p^kq" ~^k дважды продифферен;

к-о цируем обе части равенства (3.22) пор и затем, умножив нар², получим

так как р + q = 1, то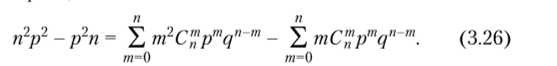

Теперь из (3.23), (3.26) следует.

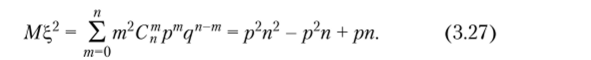
Таким образом, из (3.27) и (3.24) окончательно получим.

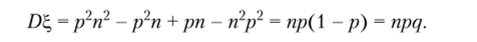
Пример 3.2. Найдем математическое ожидание и дисперсию случайной величины ?, имеющей распределение Пуассона с параметром X. Имеем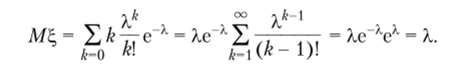

Для нахождения дисперсии воспользуемся свойством 3.7. Вычислим ML²: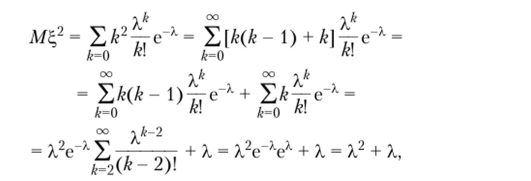

поэтому окончательно получаем.

Пример 3.3. Найдем математическое ожидание и дисперсию случайной величины, имеющей геометрическое распределение:

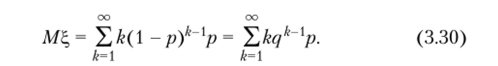
Рассмотрим степенной ряд.

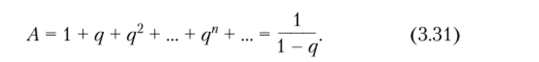
Так как 0 < q < 1, то ряд (3.31) можно почленно дифференцировать, причем.

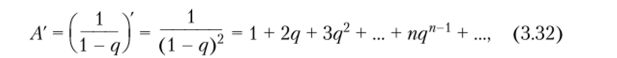
таким образом, из (3.30) и (3.32) следует, что.

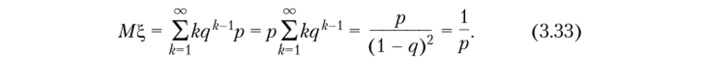
Дисперсию будем находить по формуле Найдем.

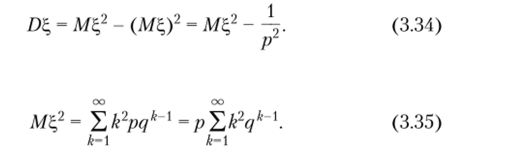
Дифференцируя ряд (3.32), получаем.

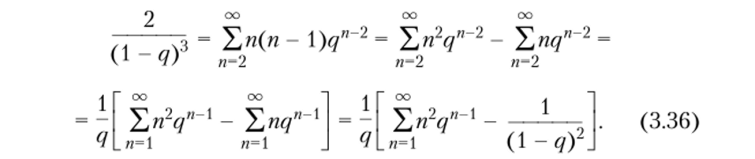
Из (3.36) следует, что.

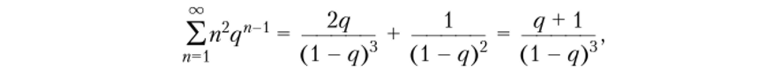
поэтому из (3.34) и (3.35) окончательно получим.

Пример 3.4. Пусть ?, — случайная величина, имеющая равномерное распределение на отрезке [а, Ь]. Найдем математическое ожидание и дисперсию ?,.

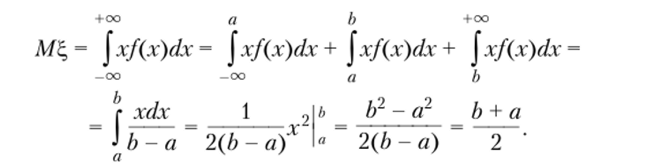
По свойству 3.8.

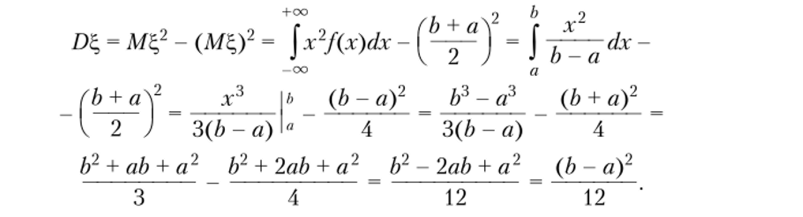
Пример 3.5. Найдем математическое ожидание случайной величины имеющей показательное распределение с параметром X. По определению математического ожидания.

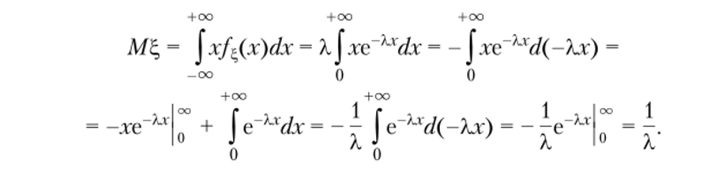
На основании свойства 3.8 имеем.

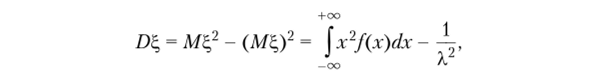
а интегрируя по частям, получим.

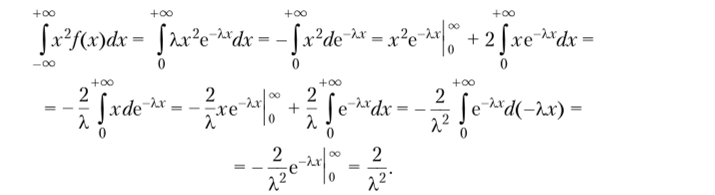
Таким образом, окончательно получим.

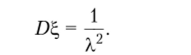
Пример 3.6. Пусть Е, — случайная величина, имеющая нормальное распределение. Покажем, что Мс = а и DE = а². Действительно.

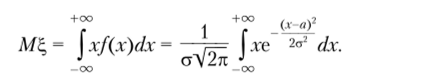
Сделаем замену переменной и получим.

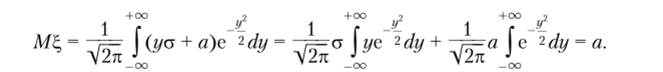
При переходе к последнему равенству учтен тот факт, что функция ус ² нечетная, следовательно,.

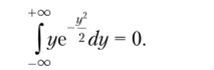
Прежде чем находить дисперсию, вычислим интеграл.

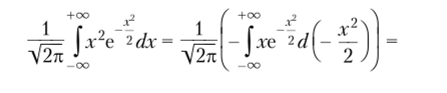
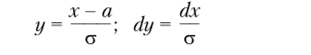
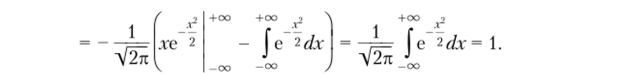
По определению дисперсии имеем.

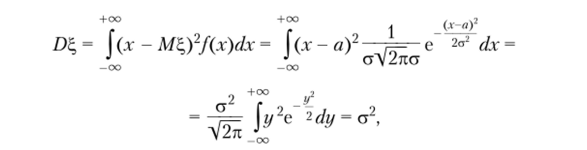
сделав замену переменной.