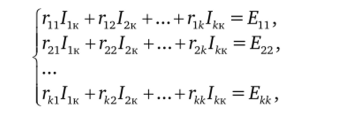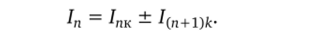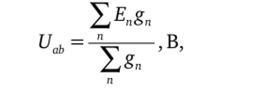Расчетные формулы для цепей постоянного тока

Методы расчета сложных цепей основываются на применении законов Ома и Кирхгофа. Сложными называют цепи, содержащие произвольное число ветвей п_в, узлов п_у, токов п_т и заданных источников ЭДС. Расчет заключается в определении токов ветвей.

Метод контурных токов (метод Максвелла)

Суть метода заключается в следующем. Выбираются независимые контуры (не перекрывающие друг друга) и направления контурных токов /_к в них. Записывается и решается система к алгебраических уравнений в соответствии со вторым законом Кирхгофа для каждого контура (к — число контуров):

где r_n" — сумма сопротивлений ветвей, входящих в контур п, п = 1,…, к; r_nj — сопротивления смежных ветвей, общих для контуров п и j, n, j = = 1,к, п *j; Е,_т — алгебраическая сумма ЭДС, включенных в ветви, образующие контур п, п = 1,…, к.

Определяются токи ветвей 1_п как алгебраические суммы (разности) соответствующих контурных токов:

Метод двух узлов

Метод двух узлов используется для цепей, имеющих п ветвей и два узла а и b (например, цепь, представленная на рис. 1.1). Узловое напряжение определяется по формуле.

где XE"g_n — алгебраическая сумма произведений ЭДС ветвей на прово;

П

димости этих ветвей; ?g_n — сумма проводимостей всех ветвей, соеди;

П

няющих узлы а и Ь.