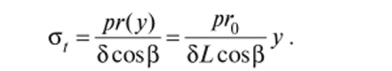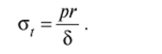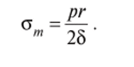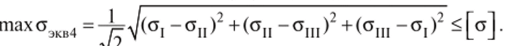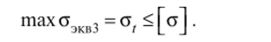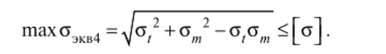Для всех тонкостенных оболочек принято ог = 0, поэтому для наиболее часто используемых в технике оболочек определим о, и от.
В сферической оболочке (рис. 13.6, а) по симметрии р, = рт = г, где г — радиус сферы ио, = о", = о.
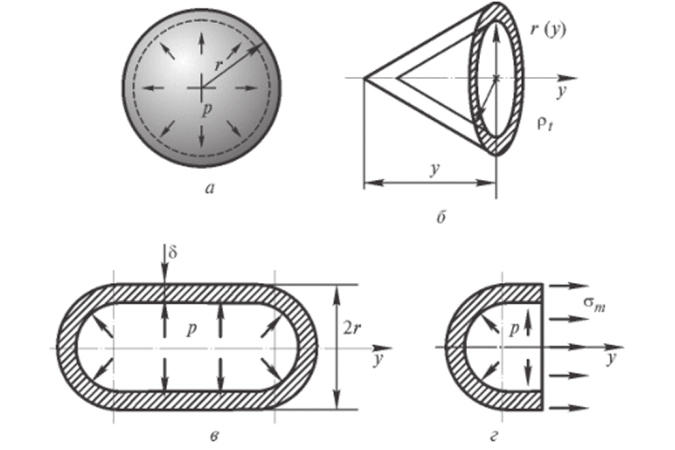
Рис. 13.6. Сферическая (а), коническая (б) и цилиндрическая (в, г) оболочки.
г (у) у
В конической оболочке (рис. 13.6, б) р", = °о, р/ =, г (у) = г0 — ,.
cos р L
где L — длина конической части оболочки. Тогда из формулы Лапласа.
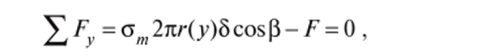
aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">
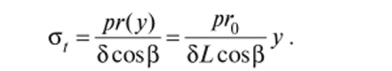
Меридиональное напряжение определяем из условия равновесия отсеченной части оболочки:
где F= лг (у)2 — сила давления газа, если сосуд находится под давлением сжатого газа, или F = 7rc^(/*(>>))f y + — вес столба жидкости, действующий на отсеченную часть оболочки, если в сосуд налита жидкость плотностью уВ цилиндрической оболочке (рис. 13.6, в) рт = 00 (образующая — прямая линия), р, = г. Тогда по формуле Лапласа о,/г+от/°° = р/Ь
Для определения меридионального напряжения о", рассмотрим равновесие отсеченной части цилиндра (рис. 13.6, г), откуда 1FX = om2nrb—pnr2 = 0 и меридиональное напряжение.
Расчет на прочность
Из выражений (13.1) и (13.2) определяем напряжения о, и от. Поскольку оболочка находится в плоском напряженном состоянии, для условия прочности необходимо определить эквивалентные напряжения. По третьей гипотезе таха.зкв3 = Oj — ат < о. По четвертой гипотезе i 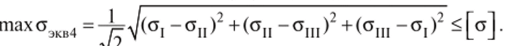
Поскольку принято расставлять главные напряжения «по росту» — Oj > о, > ош, то о, = о, о, j = о/и, ош = ог = 0. Тогда по третьей гипотезе прочности.
По четвертой гипотезе прочности.
Из условия прочности, подставив в него найденные значения напряжений, можно определить толщину оболочки при заданном давлении либо давление для заданной оболочки.


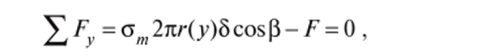 aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">
aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">