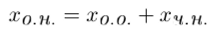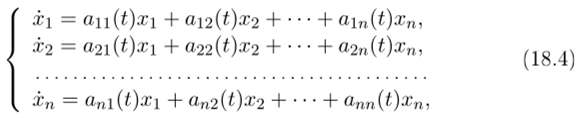Неоднородные системы. 
Дифференциальные уравнения

Общая теория линейных неоднородных систем почти идентична теории линейных неоднородных уравнений п-го порядка. Два свойства.

• • если x (t) решение неоднородной системы, a y (t) решение однородной системы, то x (t) + y (t) решение неоднородной системы и
• • если x (t) и y (t) два решения неоднородной системы, то x (t) —y (t)

решение однородной системы проверяемые простым сложением и вычитанием соответствующих тождеств, позволяют нам сформулировать следующую теорему.

Теорема 18.1 Общее решение неоднородной системы равно сумме общего решения однородной системы, и частного решения неоднородной системы^[1] :

Доказательство дословно повторяет рассуждения теоремы 10.2 из первой книги.

Однородные системы

Теорема 18.1 требует от нас сосредоточиться прежде всего на исследовании однородных систем. Однородная система имеет вид.

или в краткой записи

Опять же два ключевых свойства решений такой системы (а третье является их следствием):

• если x (t) и y (t) два решения однородной системы, то x (t) + y (t)

решение однородной системы.

• • если x (t) решение однородной системы, то для любого вещественного числа С произведение Cx (t) решение однородной системы и
• • если T¹(i), x²(t), x^k(t) решения⁴ однородной системы, то CX^l(t) + C2X²(t) + • • • + CkX^k{t) решение однородной системы

приводят нас к гипотезе о том. что общее решение однородной системы является линейной комбинацией некоторого набора решений (скорее всего, из п штук то есть в числе, совпадающем с размерностью системы) решений:

Наш опыт (приобретенный при изучении уравнений n-го порядка) уже подсказывает нам, что этот набор решений должен содержать п функций не формально, а по существу, а для этого он не должен содержать нулевых функций: функций, пропорциональных друг другу; функций, являющихся линейными комбинациями остальных. Все эти ограничения в рафинированном виде формулируются в едином математическом понятии линейной независимости. В данном случае линейной независимости вектор-функций. Ниже мы обсудим это понятие и постараемся увязать его с уже известным нам, но первому семестру свойством линейной независимости функций и известному из курса алгебры свойству линейной независимости векторов.

• [1] Наиомним, что, поскольку «общее решение51 это на самом деле множество функций, теорема устанавливает ио существу равенство двух множеств.