Матричное уравнение Ляпунова

Таким образом, наше обсуждение вопроса о поиске функции Ляпунова для системы (30.1) в виде простой функции привело нас к мысли о том. что функцию Ляпунова имеет смысл искать в виде квадратичной формы. причем для удовлетворения требованиям, предъявляемым к функции Ляпунова, эта форма (и ее матрица) обязана быть положительно определенной. Итак, мы будем искать функцию Ляпунова в виде.

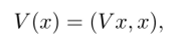
где V некоторая положительно определенная матрица. Найдем производную этой функции в силу системы (30.1). Для того, чтобы не усложнять себе жизнь вспоминанием правила дифференцирования квадратичной формы, но своему аргументу, мы просто продифференцируем по t функцию V (x (t)):

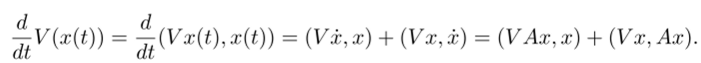
Это и есть производная нашей функции в силу системы. Нам будет удобно во втором слагаемом перенести А со второго множителя на первый, что дает, после объединения слагаемых, функцию.

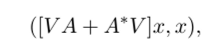
которая также оказывается квадратичной формой! Поскольку нам хотелось бы, чтобы эта форма была отрицательно определенной, мы обозначим выражение в квадратных скобочках через (-Н), превратив условие отрицательности производной функции Ляпунова в силу системы в условие положительной определенности матрицы Н. определяемой из равенства

Соотношение (30.4) обычно называют матричным, уравнением Ляпунова.

Хотя матрица Н выражается в (30.4) явным образом, термин «уравнение» на самом деле вполне уместен: не забывайте, что это пока только промежуточное соотношение, а на самом деле мы ищем матрицу V. II поэтому точное высказывание относительно (30.4) звучит так: нам надо найти две симметричные, положительно определенные матрицы V и Н, удовлетворяющие соотношению (30.4).

Уравнения с двумя неизвестными мы привыкли воспринимать как нечто, имеющее некоторую степень свободы: одну неизвестную можно задать «как попало», а другую вычислять по ней. В нашем случае неизвестными являются V и Н. II первым вариантом, который приходит в голову, является, конечно, задание произвольным образом V с вычислением Н но формуле (30.4). Это было бы хорошо, но нам мешает один пустяк: условие положительной определенности матрицы Н. Уже экспериментирование на простейших примерах (попробуйте даже на матрицах второго порядка) показывает, что добиться этого не так легко. Выход достаточно парадоксален: оказывается, надо брать произвольным образом матрицу Н, а матрицу V находить из уравнения (30.4). Как? Об этом говорит следующая теорема.

Теорема 30.2 Пусть все собственные значения матрицы, А имеют отрицательные вещественные части. Тогда, для любой симметричной положит, ельно определенной мшприцы Н существует единственная. симметричная, положительно определенная, матрица V, удовлетворяющая уравнению (НОА), и эта матрица определяется формулой

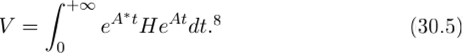
Доказательство. В формуле (30.5) стоит несобственный интеграл. Покажем, что из условия теоремы об отрицательности спектра следует, что интеграл сходится. Для этого докажем следующую лемму.

Лемма ЗОЛ Пусть все собственные значения матрицы, А имеют отрицательные вещественные части. Тогда для любого 7 > 0, такого, что Re А; < —7 <0 (г = 1,… , п), найдется такая константа М, что

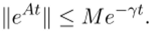
Доказательство. Матричная функция ехр (Д<) решение матричного дифференциального уравнения. Ее столбцы являются решениями ^*[1]

векторного уравнения х = Ах, и каждый ее отолбец является линейной комбинацией фундаментальной системы решений вида, предъявленного в теореме 21.6. Все эти решения являются произведениями экспонент с показателем Re Ар полиномов и тригонометрических функций. Поэтому каждый элемент матрицы exp (At) является конечной комбинацией функций вида.

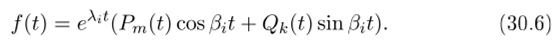
Покажем, что такие функции на бесконечности убывают как экспонента. Пусть положительное число 7 таково, что Re А; < —7 < 0. Тогда для любой скалярной функции вида (30.6) функция.

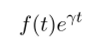
непрерывна и стремится к нулю при t —" +00^[2], поэтому она ограничена: f (t) ехр (7?)| < М, откуда мы получаем.

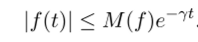
Пусть теперь функция f{t) является линейной комбинацией функций fj (t) вида (30.6). Тогда, если обозначить Мл = получаем.

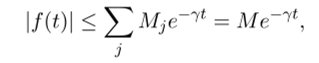
где через М обозначена сумма Mj.

Таким образом, для каждой компоненты фц (t) матричной функции Ф (?) = exp (.4i) имеем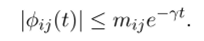

Чтобы оценить норму матричной экспоненты, преобразуем ее к виду.

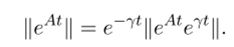
Под знаком нормы стоит матричная функция с элементами (/>jj (i)e^_7t, которые, в силу полученной выше оценки, ограничены. Но тогда, в силу того, что норма матрицы как функция от элементов матрицы непрерывна, она также будет ограничена некоторой константой^[3] М. Таким образом, получаем, что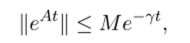

что и требовалось доказать. Лемма доказана.

Перейдем к доказательству теоремы. В силу экспоненциальной оценки на подынтегральную функцию несобственный интеграл в (30.5) сходится абсолютно. Поэтому формула (30.5) действительно дает некоторую матрицу V. Подставим ее левую часть уравнения (30.4).

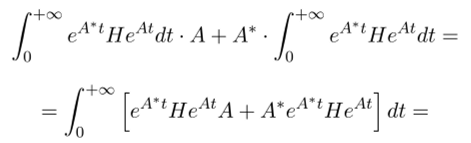
(выражение типа произведения экспоненты от матрицы на эту же матрицу мы уже встречали это производная от экспоненты).

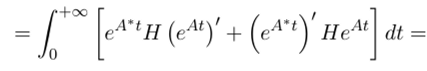
(а тут уже несложно увидеть формулу для производной произведения; слагаемое, содержащее производную среднего множителя Н отсутствует, так как эта производная равна нулю).

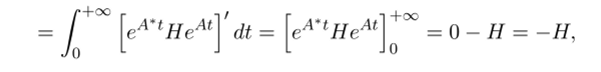
так как при t —t +оо выражение в квадратных скобочках, в силу экспоненциальной оценки, полученной в лемме 30.1. стремится к нулю, а при t — 0 экспоненты оказываются единичными матрицами. Таким образом, формула (30.5) действительно дает решение.

Покажем, что это решение единственно. Для этого возьмем уравнение (30.4), умножим его слева на ехр (АД), справа на ехр (Д?) и проинтегрируем по промежутку (0,+оо). Получим.

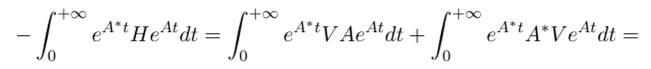
(и здесь тоже «просматривается¹⁴ полная производная произведения).

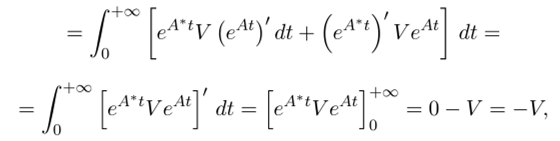
т.е. мы просто получили формулу (30.5).

Остается последний штрих показать, что определяемая формулой.

(30.5) матрица будет всегда симметричной и положительной определенной. Для этого, во-первых, просто применим операцию сопряжения (т.е.

транспонирования водь наши матрицы вещественны) к формуле (30.5). Получим.

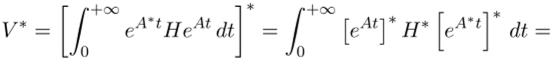
(напомним, что транспонирование меняет порядок перемножаемых матриц на обратный)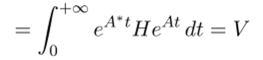

(мы воспользовались тем, что [exp (/U)]* = exp[j4*f], которое следует прямо из определения экспоненты от матрицы, и тем, что матрица II но условию теоремы симметрична: Н* = Н).

Во-вторых, найдем, как и полагается, (Уж, ж):

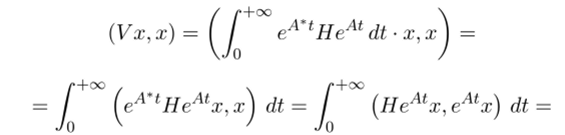
если обозначить y (t) = ехр (Л/.) • х ф О.

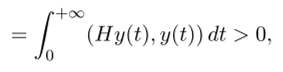
так как матрица Н предполагается положительно определенной: для всех у ф 0 выполнено (Ну, у) > 0.

Таким образом, симметричность и положительная определенность V также обоснованы. Теорема полностью доказана.

Задания для самостоятельной работы.

• 1. Выпишите матричное уравнение Ляпунова для случая неустойчивости (производная в силу системы равна нулю). Попробуйте найти решение этого уравнения в предположении, что все ReAj > 0 (при этом интеграл будет, естественно, уже по отрицательной полуоси).
• 2. Проведите рассуждения настоящей главы для случая, когда матрица А комплексная.

Каверзные вопросы.

• 1. Можно ли построить аналог функции Ляпунова для системы с переменными коэффициентами х = A (t)x в виде квадратичной формы с переменными коэффициентами? Можно ли обосновывать с ее помощью устойчивость систем с переменными коэффициентами?
• 2. Можно ли решить матричное уравнение Ляпунова в критическом случае (когда ReAj < 0 и среди ReAj есть нулевые)?
• 3. Как доказывать неустойчивость, когда не все, а только часть собственных значений матрицы А имеет положительные вещественные части?^[4]

• [1]^{Конечно,} мы сейчас «вынули зайца из шляпы». Однако эту формулу не следуетвоспринимать как фокус. В следующей главе мы объясним ее происхождение онодостаточно естественно и основывается на решении дифференциального уравненияЛяпунова матричного линейного дифференциального уравнения.
• [2] 'Ведь она является произведением экспоненты с показателем А* +7 < 0, полино-мон и тригонометрических функций.
• [3] 3начение этой константы существенно зависит от выбора нормы, но нам на самомделе она не нужна важно только то, что она существует.
• [4] Верно ли, что для неотрицательной определенности квадратичнойформы (Ах, х) необходимо и достаточно, чтобы все главные диагональные миноры матрицы, А были неотрицательны?