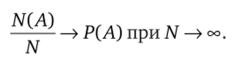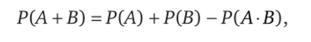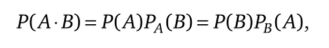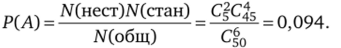Измерение вероятности. 
Теоремы сложения и умножения вероятностей

Для количественного сравнения между собой событий по степени возможности их появления вводится понятие вероятности события.

Вероятностью случайного события А называется численная мера его правдоподобия, т. е. объективная возможность появления этого события. Она обозначается через Р (Д). (Буква Р — начальная в латинском слове вероятность). Значение вероятности заключено между нулем и единицей, 0 < Р (А) < 1. Обозначим через /ДД) число тех опытов из N, в которых событие произошло (реализовалось). Отношение N (A)/N называется относительной частотой (частостью) события А в N повторениях опыта. Это статистическое определение вероятности события.

Если число повторений велико, то частота приближается к вероятности:

Это положение носит название закона больших чисел и математически доказано швейцарским ученым Якобом Бернулли (1654—1705).

Теоремы сложения и умножения вероятностей. Пусть имеем два события А и В, которые могут произойти или нет при проведении опыта. Вероятность того, что произойдет хотя бы одно из событий А или В, есть сумма вероятностей этих событий за вычетом вероятности произведения событий: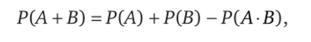

где Р (А В) — вероятность произведения событий, или вероятность того, что произойдут события и А, и В; если события несовместны, то Р (А • В) = 0 и Р (А + В) = Р (Д) + Р (В);

где Р_А (В) — условная вероятность события В, вычисленная в предположении, что имело место событие А; если события независимы, то Р_Д(В) = Р (В) и Р_Й(А) = Р (А), тогда Р (А • В) = Р (А)Р (В).

Пример 6.1.

В партии из 50 костюмов 5 нестандартных. Определить вероятность того, что среди выбранных наудачу для проверки 6 костюмов 2 окажутся нестандартными.

Решение. Число возможных способов взять 6 костюмов из 50 равно Cf₀. Интересующее событие происходит в случаях, когда из общего числа 5 бракованных костюмов взято 2 (это можно сделать С| способами), а остальные 6−2 = 4 костюма — не бракованные, т. е. взяты из общего числа 50 — 5 = 45 (количество способов равно С|₅). Поэтому число интересующих нас случаев равно С|С^₅. Искомая вероятность будет.