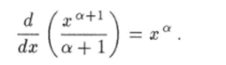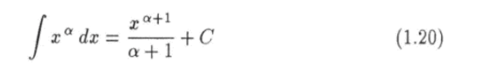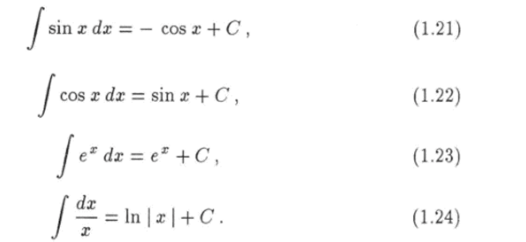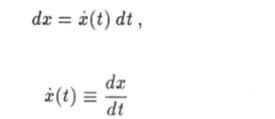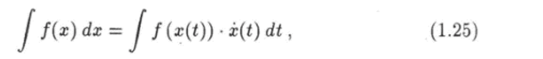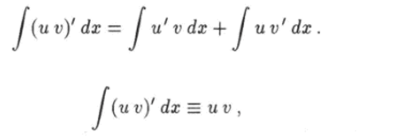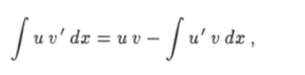Первообразная. 
Курс общей физики

Функция F (x) называется первообразной для функции /(х) на данном промежутке, если в каждой точке этого промежутка или, что эквивалентно,

Нетрудно убедиться в том, что функция F (x) + С, где С — некоторая постоянная, также является первообразной для функции /(х). Это выражение называется неопределенным интегралом от функции /(х) и обозначается символом.

здесь /(х) называется подынтегральной функцией, ах- переменной интегрирования. Отыскание первообразной, или неопределенного интеграла от заданной функции /(х) называется интегрированием этой функции. Для того чтобы проверить, правильно ли выполнено интегрирование, необходимо, как это следует из определения (1.17), продифференцировать найденную первообразную F (x) и получить подынтегральную функцию /(х).

Преобразуем формулу (1.7) при помощи прдстановки п = а+ 1. Если а ф — 1, получим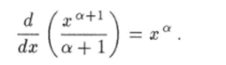

Сравнив это равенство с определением (1.17), приходим к заключению, что выражение под знаком производной есть первообразная функция x^Q, т. е.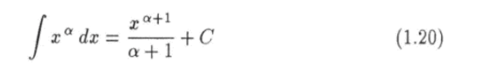

при а ф — 1. Аналогично, используя равенства (1.8) — (1.11), можно доказать следующие формулы:

Рассмотрим два метода интегрирования, первый из которых называется методом подстановки, или методом замены переменной. В этом методе для отыскания интеграла от функции f (x) вводят функцию х = x (t). Дифференциал этой функции равен.

где.

— производная от функции х по переменной t. Используя функцию я (<) и ее дифференциал, придем к формуле.

которая называется формулой замены переменной в неопределенном интеграле. Применение этой формулы имеет смысл в том случае, когда подынтегральная функция во втором интеграле проще, чем в исходном.

Другой метод называется интегрированием по частям. Проинтегрируем обе части равенства (1.13) по х. Получим.

Так как придем к формуле 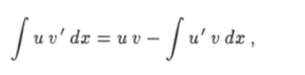которую обычно записывают в виде.

и называют формулой интегрирования по частям.