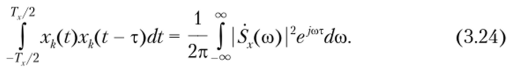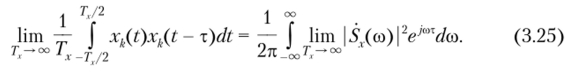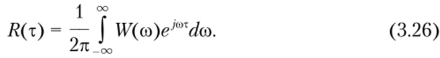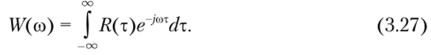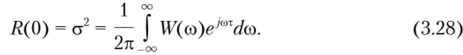Теорема Винера — Хинчина

Установим связь между корреляционной функцией и спектром мощности стационарного эргодического случайного процесса. Предварительно для этого введем модуль произведения.

TJ2.

в котором 5*((о) = | x_k{t)e/" 'dt — комплексно-сопряженная спектральная.

-TJ2

функция конкретной реализации x_k(t).

Корреляционная функция детерминированного сигнала и его энергетический спектр связаны преобразованиями Фурье. Воспользуемся формулой (3.23) и применим это свойство к отрезку конкретной реализации x_k{t) случайного процесса длительностью Т_х:

Разделим обе части равенства (3.24) на интервал Т_х. и устремим его к бесконечности:

Для эргодического процесса в левой части формулы (3.25) представлена корреляционная функция, полученная усреднением по времени; в правой части под интегралом содержится спектральная плотность мощности всего процесса (3.21). В результате получим, что корреляционная функция случайного процесса.

Это соотношение является фундаментальным в теории случайных сигналов и в некоторой мере может рассматриваться как обратное преобразование Фурье корреляционной функции. Существует и прямое преобразование Фурье.

Заметим, что отсутствие в формулах (3.26) и (3.27) и далее индексов у функций W^co) и R_r(т) показывает, что результаты справедливы по отношению ко всем случайным процессам. Соотношения (3.26) и (3.27) отражают содержание теоремы Винера — Хинчина, утверждающей, что спектр мощности и функция коррекции случайного процесса связаны между собой интегральными преобразованиями Фурье. Причем чем шире этот спектр, тем хаотичнее реализации случайного процесса. Для теоремы Винера — Хипчина справедливы свойства преобразования Фурье для детерминированных сигналов. Например, чем шире энергетический спектр случайного процесса, тем меньше интервал корреляции, и, соответственно, чем больше интервал корреляции, тем уже спектр процесса.

Применяемая на практике модель случайного процесса оказывается такой, что воспользоваться непосредственно определением дисперсии (3.22) для расчета спектра мощности не представляется возможным. Однако если при этом удается вычислить корреляционную функцию случайного процесса, то получить спектральную информацию позволяет теорема Винера — Хинчина.

Физический смысл понятия спектра мощности легко выяснить, если принять в соотношении (3.26) т = 0:

Итак, дисперсия а² (индекс х в обозначении СКО опущен), равная средней мощности флуктуаций стационарного эргодического случайного процесса, пропорциональна площади под кривой спектра мощности МД со). Размерность функции корреляции случайного процесса — | В²1, а спектра мощности — [(В²-с)/рад].