Диагностика неисправностей в системе теплового контроля стекловаренной печи

Стабильность режима работы стекловаренных печей оценивают посредством системы температурного контроля. Эта система обеспечивает измерение температур в газовом пространстве печи и расплава стекла в различных точках бассейна. При эксплуатации стекловареплых печей термоэлектрические преобразователи могут выходить из строя из-за высоких температур, агрессивности среды и ряда других факторов. В свою очередь певыявлеппые своевременно нарушения в функционировании системы теплового контроля могут привести к существенному изменению режима работы технологического агрегата и, как следствие, к уменьшению производительности и ухудшению качества вырабатываемого стекла. Рассмотрим постановку задачи диагностики функционирования системы температурного контроля, в которой использован подход нечетких множеств [20].

Информационная модель множества точек контроля температурного поля в стекломассе может быть представлена в виде графа.

Для удобства и избежания разночтений напомним понятие графа [28, 31]. В общем случае граф G состоит из конечного непустого множества X вершин х €? X и заданного множества U неупорядоченных пар и = {;r_f, Х])(и G! U) различных вершин из множества X. Каждую пару {д:*, хД (д-*, Xj е X) называют ребром графа G. В зависимости от конкретной задачи ребру графа могут приводиться в соответствие различные понятия, в частности наличие или отсутствие связи между вершинами x_t и x_j} прочность или степень влияния указанной связи.

В случае, если из конечного непустого множества X вершин формируется упорядоченный набор пар и = {л:*, xj) различных вершин, граф называют ориентированным или сокращенно — орграфом. Граф может быть представлен графически, что позволяет наглядно проследить влияние вершин друг на друга, или задан матрицей отношений, в которой каждому ребру графа ставится в соответствие число. При использовании двухзначной логики в оценке веса ребра графа это число может принимать только два значения: 0 или 1. В случае использования нечеткой логики вес ребра графа может принимать значение из отрезка (О, 11. В последнем случае приходят к понятию нечеткого графа, которое определяют следующим образом.

Пусть X — конечное непустое множество вершин графа. Тогда G (X, Г) называют нечетким графом, если для каждой вершины х X множество Г* является нечетким подмножеством универсального множества X. Множество Г* характеризуется функцией степеней принадлежности рг_х (я), которая принимает значения из отрезка [0, 1]. Величина рг_х (я) для х ЕЕ X определяет степень принадлежности х нечеткому подмножеству Г_х. В случае, если рг_х (х) для любых х X принимает значения 0 или 1, нечеткий граф G (X, Г) вырождается в обыкновенный, без петель (ребер, соединяющих каждую вершину графа саму с собой) и кратных ребер (пара вершин соединяется более чем одним ребром).

При построении информационной модели системы температурного контроля стекловаренной печи формируется нечеткий граф G (X, Г), число вершин которого должно совпадать с количеством точек контроля. Функции степеней принадлежности рг. (xj)

{x_h xj^X) характеризуют степень взаимосвязи между контролируемыми температурами стекломассы в точках измерения x_t и Xj.

Задание функций степеней принадлежности рг. (xj) может выполняться различными способами. При этом могут использоваться четкая и нечеткая классификации, экспертпые оценки •опытных технологов и стекловаров.

В случае четкой классификации и при условии, что интерес представляют величины температур, степени принадлежности могут быть определены выражением.

где б и (к) — характеристическая функция, принимающая значение 1, если температуры в точках x_t и Xj на &-м шаге измерения или обе выше, или в пределах нормы, в противпом случае характеристическая функция полагается равной нулю; N — количество измерений, выполняемых на интервале усреднения.

При непрерывном нахождении степеней принадлежности целесообразно использовать усреднение на скользящем интервале, что обеспечивается рекуррентным соотношением.

где рг_х. (xj) — степень принадлежности рг_х (xj)i вычисленная на к-м шаге измерения.

В случае нечеткой классификации степени принадлежности определим следующим образом:

где Тj (А:) — температура в /-й точке контроля на к-м шаге измерения; Тщах и Гщ1п — максимально и минимально возможные величины температур.

При непрерывном вычислении степеней принадлежности можно использовать рекуррентное соотношение.

Степени принадлежности рг. (xj) могут задаваться также на.

^х{.

оспове оценок опытпых технологов и стекловаров. Необходимо отметить, что субъективные данные о взаимосвязи температур в различных точках контроля могут дать более сложную, чем нечеткая регрессивная модель, построенная по формулам (3.31) — (3.34). В общем случае оценки рг (xj) и рг (x_t) могут быть различными, в то время как формулы (3.31) — (3.34) определяют их равными. Это объясняется особенностями движения стекломассы и передачи теплоты в расплаве стекла в бассейне печи. Оценки степеней принадлежности рг. (xj), получаемые от несколь;

^xi.

кпх экспертов, необходимо усредпить:

где рг_х. (xj) — усредненная величина степепи принадлежности, учитывающая менение всех опрашиваемых экспертов; рг^ (Xj) —.

оценка, даваемая s-м экспертом, р — число опрашиваемых экспертов, у₈ — весовой коэффициент, характеризующий степень доверия к сведениям 5-го эксперта. Весовые коэффициенты долж;

v

ны удовлетворять условию нормировки 51 Y" ⁼ ^*.

s=1.

Используя полученные степени принадлежности, можно сформировать матрицу М нечеткого отношения, которая соответствует нечеткому графу G (X, Г) информационной модели системы температурного контроля. Элементы матрицы М определяются степенями принадлежности т_и = ц_г (xj) (i, j— 1, L), где L — ко;

*i.

личество точек контроля. Отметим, что в общем случае матрица М нечеткого отношения является несимметричной.

При решении задачи диагностики неисправных точек контроля необходимо исследовать связность нечеткого графа G (X, Г).

Граф называют связным, если любая пара его вершин соединена чередующейся последовательностью вершин и ребер, причем все вершины в этой последовательности различны. По свойству связности все ориентированные графы, которым соответствуют несимметричные матрицы отношений, можно разбить па четыре класса. К первому классу относят множество U_x сильных графов, в которых из каждой его вершины можно перейти в любую другую вершину данного графа. Ко второму классу относят множество U₂ односторонних графов. Граф называют односторонним, если для каждой пары его вершин по крайней мере одна вершина достижима из другой. К третьему классу относят множество U₃ слабых графов, в которых каждая пара вершин соединена путем без учета ориентации ребер. Четвертый класс — множество U₄ несвязных графов.

Задачей исследования связности нечеткого графа является нахождение степеней принадлежности графа G к множествам U_x, U₂, U₃. Обозначим эти степени принадлежности следующим образом: щд ((г), рц, (G) и рсд (G). При этом очевидны неравенства: |цд {G) < рц, (G) < ри, (G). Знак равенства справедлив в случае, если исследуемый граф является неориентированным, а его матрица отношений М симметрична.

Используя в качестве исходной матрицу отношений Л/, вычислим матрицы:

где степени матрицы вычисляются рекуррентно: M^L = M^L~^l X X М_у М° = /; «+» обозначает операцию объединения; I — единичная матрица; Т — операция транспонирования.

Умножение матриц определим выражением.

здесь c_tJ — элемент матрицы М².

Произведение матриц в соответствии с выражениями (3.35) и (3.36) интерпретируют следующим образом [2J. Операция нахождения min определяет степень связи между вершинами x_t и xj графа G и равна степени связи наименее связанного звена. При этом рассматриваются все возможные цепи длиной L из вершины Xi в вершину Xj. Цепью графа называют чередующуюся последовательность вершин и ребэр, которая соединяет вершины x_t и.

xj. Применение операции шах позволяет находить степень связи цепи длиной L, которая имеет наибольшую степень связи.

Принадлежность изучаемого графа G к множествам U_1% U₂ и U₃ для сильных, односторонних и слабых графов соответственно определяется следующими выражениями:

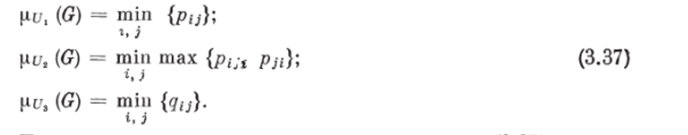
При оценке степени связности по выражениям (3.37) возможны несколько случаев. Если все рг/. (G) (i = 1,3) существенно отличны от нуля, то анализируется ри, (G). В случае, если ри, (G) близка к нулю, используются степени принадлежности ри, (G) или ри, (G). Подчеркнем, что степень связности нечеткого графа определяется наиболее слабой связью между показаниями всех пар точек контроля температуры в бассейне печи. При этом учитывается не только непосредственная связь между измерениями в каждой паре точек контроля, но и косвенные связи, реализуемые через любые другие точки контроля.

Описанная процедура вычисления матриц Р, Q и классификация изучаемого графа представляют собой процедуру идентификации информационной модели системы температурного контроля стекломассы в бассейне печи. Информационная модель предназначена для выявления неисправных точек контроля.

Для установления неисправной точки контроля из исходного нечеткого графа G (X, Г) необходимо сформировать граф 6* (Х Г'), получающийся при удалении вершины Хк из графа G (X, Г), для которого справедливо условие.

Далее необходимо определить ослабевающую вершину нечеткого графа G (X, Г). Вершину я* нечеткого графа G (X, Г) называют ослабевающей для множества U_{ в случае хи. (G) < pi/j (Gk), нейтральной при рр. (G) = pi/j (Gk), усиливающей при рц. (G) > > (&*)•.

Использование описанной процедуры для выявления неисправной точки контроля состоит в следующем. При заведомо исправной системе температурного контроля стекломассы необходимо сформировать матрицу отношений Л/, которая является информационной моделью. Далее необходимо вычислить степень связности нечеткого графа. В процессе функционирования стекловаренной печи необходимо уточнять элементы матрицы Л/ и величины степеней принадлежности рu_i (G). В случае уменьшения рu_i (G) ниже заданного порогового значения следует определить ослабевающую вершину. Помер ослабевающей вершины покажет точку контроля, подлежащую поверке. Величина порогового значения |А (/. (G) может быть определена из опыта эксплуатации конкретной печи.

Рассмотренные в главе задачи показывают, что для достаточно простых техпологпческих процессов и целей исследования обычно не акцентируют внимание на качественном этапе системного анализа. В этом случае используют модели в «точной» формулировке. В более сложных случаях роль качественной информации возрастает. Для формализации таких сведений эффективным является подход нечетких множеств. Отметим, что классификация технологических процессов на простые и сложные является нечеткой, в основе которой лежит общий уровень знаний о конкретной технологии, степень сложности взаимосвязей между различными физико-химическими эффектами, квалификация исследователя и другие. Поэтому такая классификация не имеет строгого количественного выражения.

Возможность учета информации, получаемой из различных источников, простота формализации и объединения таких сведении па начальных этапах построения моделей показывают, что подход нечетких множеств позволяет проводить декомпозицию сложных объектов исследования па отдзльпые физико-химические процессы. При этом выделяются интересующие явления. Построение функций степеней принадлежности обеспечивает учет влияния других факторов на выделенное явление.