Методика изучении линейных уравнений с одним неизвестным

Линейные уравнения с одним неизвестным — это первый класс уравнений в курсе алгебры, поэтому от характера его изучения в значительной мерс зависят особенности организации всего последующего изучения линии уравнений и бб неравенств. При изучении этого класса уравнений формируется общее понятие об уравнении, вводится соответствующая терминология.

Первая методическая задача, с которой сталкивается учитель, приступая к изложению этой темы, состоит в выделении формальной части понятия уравнений из той ситуации, в которой оно возникает. В качестве такой ситуации обычно выступает несложная текстовая задача, решение которой алгебраическим методом приводит к уравнению первой степени с одним неизвестным. Здесь следует обратить внимание учащихся на основной метод, примененный в решении задачи, — переход к её алгебраической модели, общий вид которой f (х) = g (х), где/и g — некоторые выражения, содержащие неизвестное л;.

Проследим, как реализуется этот этап на практике, например, по учебнику Макарычева Ю. Н. и др. «Алгебра. 7 класс» (М., 2014). Сначала решается задача: «На нижней полке в 4 раза больше книг, чем на верхней. Если с нижней полки переставить на верхнюю 15 книг, то книг на полках станет поровну. Сколько книг на верхней полке?

Обозначим буквой * число книг на верхней полке. Тогда число книг на нижней полке равно 4*. На нижней полке останется: Ах - 15 книг, а на верхней будет* + 15 книг. По условию задачи после такой перестановки книг на полках окажется поровну. Значит,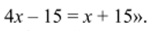

Далее учитель говорит: «Чтобы найти неизвестное число книг, мы составили равенство, содержащее переменную. Такие равенства называют уравнениями с одной переменной или уравнениями с одним неизвестным. Нам надо найти число, при подстановке которого вместо * в уравнение 4* - 15 = * + 15 получается верное равенство. Такое число называют решением уравнения или корнем уравнения». Затем формулируется определение.

Опр. 1. Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.

Учащиеся убеждаются, что уравнение 4х- 15 =х + 15 имеет один корень — число 10. Затем выясняется, что можно привести примеры уравнений, которые имеют два, три и более корней или не имеют корней.

Так, уравнение (* - 4)(* - 5)(х — 6) = 0 имеет три корня *, = 4, *₂ = 5, *з⁼ 6.

Уравнение * + 2 = * нс имеет корней, так как при любом значении * левая часть уравнения на 2 больше его правой части. В результате делается вывод: «Решить уравнение — значит найти все его корни или доказать, что корней нет».

Замечание. В различных учебниках применяется разная терминология, относящаяся к одному и тому же классу уравнений. Поэтому надо быть внимательным и употреблять только те термины, которые введены в учебнике, причем, именно в том смысле, который им придается.

Рассмотрим теперь несколько подходов к выделению первого изучаемого в курсе алгебры класса уравнений.

1. В учебнике Ю. Н. Макарычева и др. «Алгебра. 7 класс» (М., 2014) — это линейные уравнения с одной переменной, то есть уравнения вида ах = Ь, где * -переменная, а и Ь - числа. Это определение выделяет очень узкий класс уравнений, недостаточный для решения самых простых задач. Какую роль он выполняет?

Во-первых. уравнения этого класса решаются просто, причем этот класс допускает полное исследование (что и осуществляется в учебнике). Во-вторых. запись уравнений из этого класса играет роль образца, к которому могут быть сведены посредством простейших преобразований уравнения более широкого класса.

В учебнике проводится исследование линейного уравнения с одной переменной ах = b:

1) если а Ф 0, то уравнение ах = b имеет единственный корень х=

а

• 2) если а = О, b ф 0, тогда 0 • х = Ь Ф 0, и уравнение ах = b не имеет корней;
• 3) если а = О, b = 0, тогда 0 • х = 0 при любом х, поэтому уравнение ах= b имеет бесконечно много корней.

Далее рассматриваются случаи сведения уравнения к линейному.

Большая часть времени, отводимого на изучение линейных уравнений по этому учебнику, используется именно на то, чтобы сформировать навыки сведения к линейным других уравнений, не входящих в этот класс.

2. В учебнике Ю. М. Колягина и до. «Алгебра. 7 класс» (М., 2012) вводится и рассматривается класс уравнений, названный по-иному — уравнения первой степени с одним неизвестным. К особенностям введения этого класса следует отнести то, что явного определения он не получает: определение заменяется описанием и иллюстрацией несколькими примерами. Предполагается, что в итоге их рассмотрения учащиеся получат ясное представление об объёме понятия.

Сначала рассматривается задача: «Конверт с новогодней открыткой стоит 17 р. Конверт дешевле открытки на 5 р. Найти стоимость открытки.

Пусть открытка стоит.* р., тогда конверт стоит (.* - 5) р. По условию задачи х + (х — 5) = 17, откуда 2х — 5 = 17, 2х — 22, х = 11.

В равенстве х + (х — 5) = 17 буква л* обозначает неизвестное число, или, короче, неизвестное". Затем формулируется определение.

О/?/;. 2. Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением.

Онр. 3. Корнем уравнения называется то значение неизвестного, при котором это уравнение обращается в верное равенство.

Решить уравнение — это значит найти все его корни или установить, что их нет.

Далее сообщается, что решение многих практических задач сводится к решению уравнений, которые можно преобразовать в уравнение.

где а и b — заданные числа, х — неизвестное. Уравнение (1) называют линейным уравнением.

Основное внимание в учебнике Ю. М. Колягина и др. уделяется изложению правил последовательного преобразования уравнения ко все более простому виду. Фактически при этом приходят к уравнению ах = Ь. Этот класс уравнений явно не выделяется, но на примерах рассматриваются все возможные случаи решения уравнений из него. Такой подход позволяет сконцентрировать внимание непосредственно на алгоритмах решения уравнений.

3. В учебнике Л. К. Фаддссва «Алгебра 6−8. Материалы для ознакомления» (М., 1983) также вводится понятие уравнения первой степени с одним неизвестным и объясняется алгоритм его решения. В отличие от учебника Ю. М. Колягина и др. здесь дано явное определение этого уравнения.

Опр. 4. «Алгебраическое уравнение от одного неизвестного называется уравнением первой степени, если обе его части являются многочленами первой степени относительно неизвестного».

4. В учебнике С. М. Никольского. М. К, Потапова «Алгебра: Пособие для самообразования» (М., 1984) в системе изучения присутствуют оба понятия: и линейные уравнения с одним неизвестным, и уравнения первой степени.

Введение

двух терминов (линейное уравнение и уравнение первой степени) позволяет четче описать сам процесс решения. Однако при этом возникает необходимость в усвоении двух, а не одного термина. Точно так же указание явного определения изучаемого понятия по сравнению с описанием имеет преимущество большей четкости, но предъявляет более высокие требования к развитию логического мышления учащихся.

Выделенные 4 варианта изложения теории уравнений, имеющих вид ах + b = сх + d, свидетельствуют о том, что эта теория допускает несколько различных по стилю и методике изучения развертываний.

Можно (как это сделано в 1-ом и 4-ом случаях) сконцентрировать внимание на выделении более узкого класса, играющего роль «канонического вида», к которому приводятся данные уравнения; но можно (как во втором и третьем случаях) обойтись и без этого, а сразу изучать способы решения уравнений общего класса, используя изученные типы преобразований уравнений. Точно так же можно по-разному описывать вводимые термины: четким определением или же посредством описания.

Несмотря на наличие таких разных подходов к введению первого класса уравнений, основная часть методики его изучения одинакова при любом из них. Это объясняется прежде всего тем, что основной целью изучения в данном случае всегда является освоение правил решения уравнений данного класса (в основном они относятся к преобразованиям буквенно-числовых выражений).

В итоге изучения первого класса уравнений учащиеся должны овладеть: алгоритмом решения уравнений данного класса; умением применять результаты исследования уравнений данного класса; основными понятиями общей теории уравнений; применением уравнений данного класса к решению текстовых задач.