Введение понятия равных треугольников

Треугольник — самый «экономный» вид многоугольника. Для его задания достаточно указать его вершины — три точки, не лежащие на одной прямой, или три попарно пересекающиеся прямые. Классифицируют треугольники или по степени их симметричности или по числу равных сторон (таблица 9).

Таблица 9.

В школе принята также классификация треугольников по углам: остроугольные, прямоугольные и тупоугольные.

Изучение треугольников в соответствии с программой распределено по всем классам основной школы. Курс 7 класса — это, по существу, геометрия треугольника.

Треугольник — одна из основных «рабочих» фигур изучаемого в школе курса планиметрии. Установление цепочек равных треугольников — широко используемый прием доказательства различных геометрических утверждений.

Равенство треугольников традиционно изучается в курсе планиметрии. Однако трактовка этого понятия, методика его введения разные для различных учебников. Так, в учебниках А. Н. Колмогорова и др. «Геометрия 6−8» (М., 1979) и Л. С. Атанасяна и др. «Геометрия 7−9» (М., 2003) равные треугольники — частный случай равных фигур, то есть фигур, которые можно совместить наложением. Такие понятия, как «совмещение» и «наложение», считаются интуитивно понятными учащимся и в курсе не определяются.

Иной подход, как уже было сказано, реализован в пробном учебнике А. Д. Александрова и др. Здесь равными называются треугольники, у которых соответственные стороны равны. Такая «экономия» свойств, определяющих равные треугольники, ведет к сокращению числа признаков равенства треугольников. С другой стороны, такой подход не позволяет ввести общее понятие равных многоугольников.

Будем рассматривать методику изучения равенства фигур по действующим учебникам А. В. Погорелова и Л. С. Атанасяна и др., хотя методические рекомендации по формированию понятий, по организации работы с теоремой применимы и к изучению этой темы по другим учебным пособиям, в частности по учебнику А. Д. Александрова и др. (Подробно этот вопрос рассмотрен в учебном пособии Г. И. Саранцева [11].).

1. Учебник геометрии А. В. Погорелова

Характерным для учебника А. В. Погорелова является наличие в нем аксиомы существования треугольника, равного данному (которая, по существу, является эквивалентом аксиомы подвижности плоскости).

Понятие равных отрезков (углов) можно ввести здесь следующим образом. Начертить на доске несколько отрезков, среди которых должны быть и такие, которые имеют равные длины, измерить длины отрезков, отметить, что отрезки, имеющие одинаковую длину, называются равными.

Определение равных отрезков простое и поэтому не требуется большой работы для его усвоения. Для этого достаточно выполнить следующие упражнения:

• 1. Установить с помощью линейки, какие из изображенных на рисунке отрезков равны (рисунок дан).
• 2. Известно, что отрезок А В равен отрезку CD. В каком соотношении находятся их длины?

При введении понятия равных треугольников следует начертить несколько треугольников, измерить их стороны и углы, выделить треугольники с равными углами и сторонами, это равные треугольники. Затем следует предложить упражнения на усвоение существенных свойств понятия, в частности, на усвоение записи равенства треугольников.

1. Что нужно знать, чтобы утверждать равенство треугольников АВС и DE/C?

Рис. 55.

• 2. На рисунке 55 изображено два равных треугольника. Написать равенство этих треугольников, обозначив их вершины.
• 3. Если разносторонние треугольники АВС и DKM
• (рис. 56) равны, то
• а) АВ = DK, АС = DM, ZB = ZK;
• б) zA = ZM, AB = DK, ZC= zD;
• в) AB = DK, AC — DM, BC = KM, ZA — ZD, ZB = ZК! Верны ли эти утверждения?

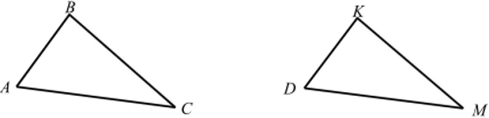
Рис. 56.

• 4. Известно, что ДАВС = АМРК. Написать все соотношения между сторонами и углами этих треугольников.
• 5. Известно, что ZA = ZK, ZB = ZL, ZC= ZM, AB = KL, AC = KM, BC = LM. Равенство каких треугольников следует из условия?
• 6. ZA = ZP, ZB = ZL, ZC = ZM. Равны ли треугольники АВС и PLM? Дополнить условие так, чтобы из него следовало равенство треугольников АВС и PLM.

Следует обратить внимание на запись равенства треугольников в данном учебнике. Буквы, обозначающие соответственные вершины, должны занимать одинаковые позиции в обозначении треугольников. Это позволяет: 1) имея запись равенства треугольников, например, А АВС = A PQR, почти автоматически делать вывод о равенстве соответственных сторон и углов, т. е. по определению будем иметь: AB = PQ, ВС = QR, АС = PR, ZA = ZP, ZB = ZQ, ZC = ZR 2) существенно опираться на запись равенства треугольников при доказательстве равенства углов при основании в равнобедренном треугольнике и теоремы, обратной ей.

Необходимо отметить, что А. В. Погорелов использует (в целях логического развития учащихся) сильный прием: доказательство эквивалентности двух различных определений равных треугольников — вышеуказанного и как фигур, совмещаемых движением. Этот вопрос можно обсудить на занятиях кружка или в индивидуальной работе с сильными учащимися.

1. Учебник геометрии Л. С. Атанасяна и др.

В этом учебнике понятие равных фигур вводится через наложение. Для этого на листе бумаги изображаются две равные фигуры Ф] и Ф₂, затем копируется фигура Ф| на кальку и перемещением кальки совмещается копия фигуры Ф| с фигурой Ф₂. Если они совместятся, то фигура Ф] равна фигуре Ф₂. (Подобные действия можгго проиллюстрировать с помощью компьютера.).

Согласно определению равенства фигур два отрезка (угла, треугольника) равны, если их можно совместить наложением. Для усвоения этих понятий следует использовать упражггеггия на установление равенства заданных фигур с помощью кальки. Таким же способом легко установить, что: а) равные отрезки имеют равные длины и обратно; б) равные углы имеют равные градусные меры и обратно. Эти утверждения используются для доказательства равенства отрезков, углов.

Программа диктует необходимость с самого начала изучения курса планиметрии проводить с учащимися работу по формированию и развитию таких понятий, как «свойство» и «признак».

После введения определения равных треугольников обычно рассматривается их свойство: «В равггьгх трсугольггиках против равггьгх сторогг лежат равные углы и против равных углов лежат равные стороны». Из такой формулировки ученику непонятно, что же здесь дано, а что требуется доказать. Поэтому желательно формулировку теоремы дать на языке «если — то»: «Если треугольники равны, то …». Ученику видно, что даны равные треугольники, и в этом случае легче пояеггить, что речь идет о свойствах равггьгх трсугольг г и ков. Когда заключение в формулировке теоремы будет «…, то такие треугольники равны», то следует заметить учащимся, что речь идет о признаке равных треугольников.

Цслссообразгго также выполнить ггссколько упражнений гга доказательство равенства фигур с помощью наложения. Такие упражнения будут способствовать усвоению метода доказательства, который используется в учебнике.

1. ААВС = ДЛ|#|С|. Докажите, что медианы BD и BD этих треугольников равны.

Так как АЛВС = ЬАВС, то при наложении треугольника АВС на треугольник АВС вершины А, В, С совпадут соответственно с вершинами А, В_и С|. Так как точки D и D середины совпавших сторон АС и АС, то при указанном наложении они также совпадут, следовательно, совпадут и отрезки BD и BD. Значит, BD = BD.