Методика изучения линейной функции

Место темы «Линейная функция» и последовательность изложения материала в разных учебниках разная (см. таблицу 8).

Таблица 8.

Как видим, по учебнику Ю. Н. Макарычева и др. линейная функция изучается в начале курса, что дает возможность раньше использовать её график (например, при решении уравнений или неравенств), а по учебнику Ю. М. Колягина и др. она изучается в конце курса. Кроме того, в нем не выделен пункт «Взаимное расположение графиков линейных функций», очень важный для графического решения систем уравнений. В первом учебнике сначала изучается линейная функция, а затем, как частный случай, прямая пропорциональность (у = кх). Во втором учебнике сначала изучается функция у = кх, а затем линейная функция и её график.

Рассмотрим более подробно методику введения линейной функции и её графика (в первом варианте). Изучение линейной функции начинается с рассмотрения конкретных примеров:

Пример 1. На шоссе расположены пункты А и В, удаленные друг от друга на 20 км (рис. 39).

Рис. 39.

Мотоциклист выехал из пункта В в направлении, противоположном Л, со скоростью 50 км/ч. За / часов мотоциклист проедет 50/ км и будет находиться от А на расстоянии (50/ + 20) км.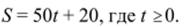

Пример 2. Ученик купил тетради по 3 р. за штуку и ручку за Зр. 50 к. Стоимость покупки зависит от числа тетрадей.

Обозначим число купленных тетрадей буквой х, а стоимость покупки (в руб.) буквой V. Получим: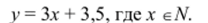

Пример 3. Из курса физики известно, что если железная проволока длиной 1 м нагревается до температуры /°, а коэффициент линейного се расширения равен к = 0,0012, то длина проволоки при этой температуре может быть вычислена по формуле.

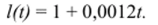
И т. д.

В этих примерах мы встретились с функциями, заданными формулами вида у = кх + Ь, где х — независимая переменная, к и b — числа. Такие функции называют линейными.

Затем формулируется определение.

Опр. /. Линейной функцией называется функция, которую можно задать формулой у = кх + Ь, где х — независимая переменная, kwb- некоторые числа.

Усвоение определения происходит путем выполнения упражнений на распознавание. После этого учащиеся знакомятся с графиком линейной функции. При этом рассматриваются два наиболее распространенных способа построения графика линейной функции.

1 способ. Использование «загущения» точек на графике. Последовательность действий по этому способу: а) нанесение нескольких точек; б) наблюдение — все построенные точки расположены на одной прямой; проведение этой прямой; в) проверка: берем произвольное значение аргумента и вычисляем по нему значение функции; наносим точку на координатную плоскость — она принадлежит построенной прямой. Отсюда делается вывод о графике данной линейной функции.

Общее свойство линейных функций будет при этом формироваться на основе изолированных примеров.

2 способ. Построение графика по двум точкам. Этот способ уже предполагает знание соответствующего свойства графиков линейных функций.

В обучении происходит последовательная смена этих способов: когда общее свойство графиков усвоено (при рассмотрении первого способа), начинают применять второй способ — он экономнее и обоснован геометрически, так как через две точки проходит одна и только одна прямая.

Изучение этих способов сопровождается рассмотрением конкретных примеров.

Пример 1. Построить график линейной функции у = 0,5дг — 2.

Составим таблицу соответственных значений .v и у:

Отметим в координатной плоскости точки, координаты которых указаны в таблице. Все отмеченные точки лежат на одной прямой. Эта прямая является графиком линейной функции у = 0,5* - 2 (рис. 40 а, б).

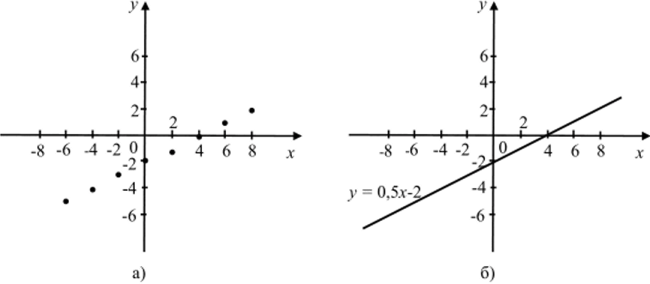
Рис. 40.

После этого делается вывод, что графиком любой линейной функции является прямая. Для построения графика линейной функции достаточно найти координаты двух точек графика, отметить эти точки в координатной плоскости и провести через них прямую.

В качестве упражнений можно рассмотреть примеры на построение графика линейной функции: )у = 2х + 3; 2) у = -0,8jc + 1.

Замечание 1. В7 классе принимают без доказательства тот факт, что графиком линейной функции является прямая линия. В 8 классе после изучения признаков подобия треугольников появляется возможность обосновать этот факт (попробуйте провести доказательство самостоятельно).

Замечание 2. Если область определения линейной функции состоит не из всех чисел, то её график представляет собой соответствующую часть прямой. Например, это может быть полупрямая или отрезок.

Влияние коэффициентов к и b на поведение функции

1. При к = 0 формула у = кх + b имеет вид у = 0. v + b, то есть у = Ь. Линейная функция, задаваемая формулой у = b, принимает одно и то же значение при любом Ху например, функция у = -2 принимает значение -2 при любом х. Функция у = b — это частный случай линейной функции. Ее графиком является прямая, параллельная оси ОХ и проходящая через точку (0; -2).

Для учащихся построение графика функции у = b представляет определенную трудность психологического характера, так как в такой формуле в явном виде не содержится переменная х. Поэтому можно рекомендовать записывать формулу у = b в виде у = Од: + b, тогда, как и в общем случае, учащиеся смогут находить пары соответственных значений х и у. (При этом в качестве х берется любое число, а значение у при любом х оказывается равным Ь.)

Желательно, чтобы на первых же уроках учащиеся усвоили, что графиком функции у = b служит прямая, параллельная оси ОХ, и что при b = 0 мы получаем саму ось ОХ.

2. Вторым частным случаем линейной функции является прямая пропорциональность.

Введение

прямой пропорциональности осуществляется следующим образом. Рассматривается пример: пусть V — объем железного бруска в см³, т — его масса в г. Так как плотность железа равна 7,8 г/см³, то т = 7,8 V.

Зависимость массы железного бруска от его объема является примером функции, которая задается формулой вида у = кх, где х — независимая переменная, к — число, отличное от нуля. Такую функцию называют прямой пропорциональностью. Затем формулируется определение.

Опр. 2, Прямой пропорциональностью называется функция, которую можно задать формулой вида у = кх, где х- независимая переменная, к — число, отличное от нуля.

Учащимся сообщается, что прямая пропорциональность является частным случаем линейной функции, так как формула у = кх получается из формулы у = кх + b при Ь = 0. Отсюда следует, что графиком прямой пропорциональности служит прямая. Эта прямая проходит через начало координат, так как при х = 0у = 0.

Итак, графиком прямой пропорциональности является прямая, проходящая через начало координат.

Для построения графика прямой пропорциональности достаточно отмстить какую-либо точку графика, отличную от начала координат, и провести через эту точку и начало координат прямую. (Учащимся предлагается построить график функции у = 0,5л:.).

Расположение графика функции у = кх в координатной плоскости зависит от коэффициента к. Из формулы у = кх находим, что если х = 1, то у = к. Значит, график функции у = кх проходит через точку (1; к). При к > 0 эта точка расположена в первой координатной четверти, а при к < 0 — в четвертой. Отсюда следует, что при к > 0 график прямой пропорциональности расположен в I и III координатных четвертях, а при к< 0 — во II и IV четвертях.

Итак, обучив семиклассников построению графика линейной функции, можно приступить к элементарному исследованию свойств этой функции. В 7-м классе возможно аналитически выделить значения аргумента, при которых линейная функция принимает положительные (отрицательные) значения, доказать монотонность линейной функции. Все остальные свойства (например, роль и геометрический смысл коэффициентов в уравнении линейной функции) можно установить из геометрических соображений.

Достаточно легко устанавливается, что коэффициент b есть значение линейной функции при х = 0. Геометрически b означает длину и положение на оси ординат отрезка, отсекаемого графиком функции, считая от 0 (вверх, если b > 0, и вниз, если b < 0) или иначе, это ордината точки пересечения графика функции с осью OY (абсцисса этой точки всегда равна 0). А коэффициент к находится в случае прямой пропорциональности у = кх как к = у (1), В общем случае линейной функции как к = у () — Ь. Учащимся следует все это показать на графиках функций (рис. 41 а, б).

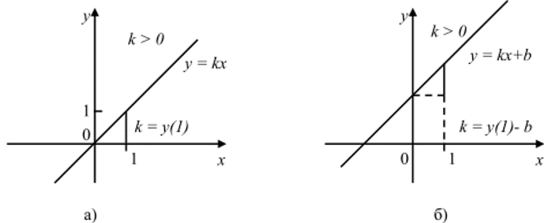
Рис. 41.

Значительные трудности представляет случай отрицательных значений углового коэффициента; для него требуется отдельная работа, построенная аналогично.

Конечно, необходимы упражнения в отыскании коэффициентов линейной функции по их графикам. Начальные упражнения должны быть простыми и иметь своей целью усвоение геометрического смысла коэффициентов формулы, задающей функцию. Приведем примеры.

1. Найдите значения коэффициентов к в уравнениях прямых у = кх, изображенных на рисунке 42. Запишите уравнения этих прямых.

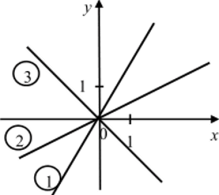
Рис. 42.

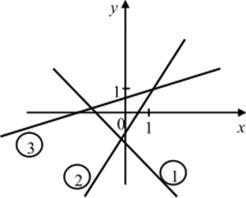
Рис. 43.

• 2. а) Найдите значения коэффициентов b для прямых у = кх + Ь, изображенных на рисунке 43.
• б) Каковы числовые значения коэффициентов к для этих прямых с точностью до 0,1?
• в) Запишите уравнения прямых, изображенных на этом рисунке (измерения дадут приближенные значения к и b).

Графические иллюстрации приводят учащихся к выводу, что при к > О график линейной функции составляет острый угол с положительным направлением оси абсцисс, а при к < 0 — тупой угол.

После этого можно говорить о возрастании и убывании линейной функции в зависимости от знака коэффициента к. Сказанное можно закрепить в упражнениях.

• 3. Не строя графиков функций, установите, под острым, тупым или нулевым углом они наклонены к положительному направлению оси абсцисс:
  • а) у = *; б)>> = -*+1; в) у = 2; г)>> = 10,7*-5.
• 4. Даны функции:
  • а)д> = 2* + 4; б) у = 2х- 4; в) >> = -2*+ 4; г) д> = -2*-4.

Не строя графиков, выясните, в каком случае значения у возрастают (убывают) с возрастанием х. Затем постройте графики и проверьте на них свои ответы.

Выполняя такие упражнения, учащиеся постепенно овладевают умением «читать» график, готовятся к элементарному исследованию функции у = кх + Ь. Эти упражнения являются также подготовкой к более серьезному изучению в дальнейшем геометрического смысла и роли коэффициентов квадратичной функции.

Таким образом, при изучении линейной функции предпочтение отдается графическим методам, поскольку основной аппарат для аналитического исследования функции (неравенства) ещё нс изучен. Восприятие графических иллюстраций, и даже суждений и умозаключений, из наблюдения и анализа геометрических представлений более доступно семиклассникам, чем выполнение ими логических аналитических умозаключений.

Аналогично можно провести исследование роли коэффициента к в формуле у = -, задающей обратную пропорциональность. Но при этом надо учи- х

тывать, что рассматриваемая функция имеет разрыв при х = 0. (Проведите это исследование самостоятельно и сделайте выводы.).

Взаимное расположение графиков линейных функции

Графики двух линейных функций представляют собой прямые, которые либо пересекаются, либо параллельны. Установить с учащимися этот факт можно следующим образом. Рассмотрим, например, графики функций, заданных формулами у = 0,9* - 1 и у = 0,8* + 1 с различными коэффициентами при*. Выясним, пересекаются ли эти графики. Пересечение графиков означает, что они имеют общую точку. В этом случае найдется такое значение *, которому соответствует одно и то же значение у для обеих функций. Чтобы найти это значение *, надо решить уравнение:

0,9*- 1 =0,8*+ 1.

При * = 20 обе функции у = 0,9* - 1 и у = 0,8* + 1 принимают одно и то же значение, равное 17. Точка (20; 17) принадлежит как одному, так и другому графику. Такая точка только одна. Значит, прямые, являющиеся графиками функций у = 0,9 т — 1 и у = 0,8 т + 1, пересекаются.

Рассмотрим теперь линейные функции, заданные формулами у = 0,5 т + 4 и у = 0,5 т — 2 с одинаковыми коэффициентами. Так как уравнение.

0,5 т + 4 = 0,5 т — 2.

нс имеет корней, то прямые, которые являются графиками функций у = 0,5 т + 4 и у = 0,5 т — 2 не имеют общих точек, то есть они параллельны.

Вообще, графики двух линейных функций, заданных формулами вида у = кх + Ь, пересекаются, если коэффициенты при х различны, и параллельны, если коэффициенты при х одинаковы.

Графики линейных функций, заданных формулами у = kx + b с одинаковыми коэффициентами при т и различными b, параллельны и наклонены к оси От под одним и тем же углом. Этот угол зависит от коэффициента к. Число к называют угловым коэффициентом прямой — графика функции;' = кх + Ь.

Это свойство можно сформулировать так: если угловые коэффициенты прямых, являющихся графиками двух линейных функций, различны, то эти прямые пересекаются, а если угловые коэффициенты одинаковы, то прямые параллельны.

Из формулы y = kx + b следует, что при т = 0, у — Ь. Значит, график функции;' = kx + b пересекает ось Оу в точке с координатами (0; Ь).

Чтобы далее выяснить, как располагаются графики функций y — kx + b при различных значениях к и одинаковых значениях b, можно предложить учащимся упражнение: постройте графики функций: у = 2х + 3, у = 0,5 т + 3, у = -Зт + 3. После построения учащиеся делают вывод, что все эти прямые пересекаются в одной точке, лежащей на оси Оу.

Основные типы упражнений к этой теме следующие:

• 1. Установить взаимное расположение графиков функций (функции заданы формулами).
• 2. Линейные функции заданы формулами. Выделить те функции, графики которых: а) параллельны; б) пересекаются.
• 3. Дана линейная функция (например: у = 2,5 т + 4). Задайте формулой какую-нибудь линейную функцию, график которой
• а) параллелен графику данной функции;
• б) пересекает его.
• 4. Задать формулами две линейные функции, графики которых:
  • а) параллельные прямые; б) пересекающиеся прямые.
• 5. Найти координаты точки пересечения графиков функций (функции заданы формулами).

В результате выполнения упражнений учащиеся должны знать, как располагается график функции у = kx + b в зависимости от значений к и Ь.