Параметрические зависимости. 
Инженерная 3d-компьютерная графика

Параметризацию объектов можно, как и ранее, выполнять в классическом интерфейсе (рис. 26.1). Однако целесообразно перейти к ленточному интер;

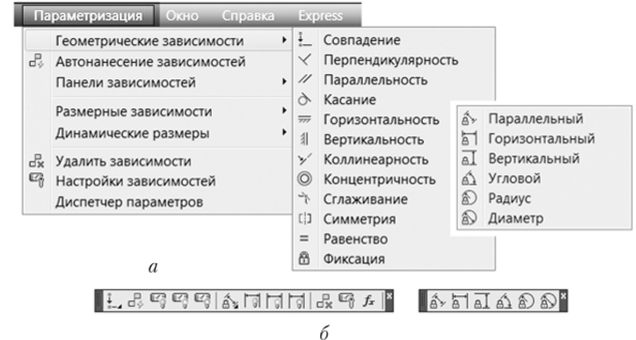
Рис. 26.1. Классический интерфейс параметризации:

а — разделы меню; 6— панели инструментов фейсу (см. п. 1.5 «Лента» и рис. 1.5) как более адаптированному к этому типу задач:

• ? перейдите к ленточному интерфейсу, либо выполнив команду ribbon (Лента), либо сменив рабочее пространство на Рисование и аннотации. В итоге возникла лента инструментального интерфейса (см. рис. 1.5);
• ? укажите в ленте вкладку Параметризация — возникли инструментальные панели (рис. 26.2).

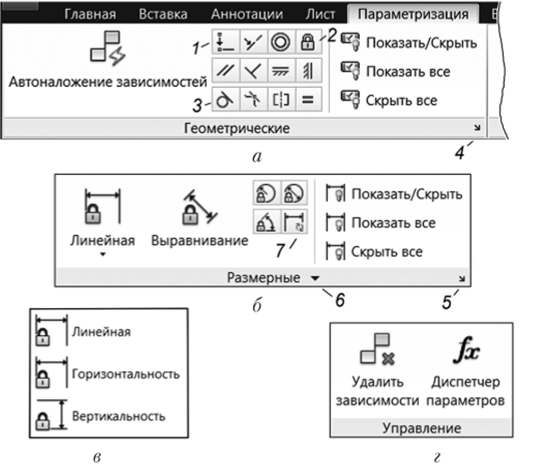
Рис. 26.2. Ленточный интерфейс параметризации

Геометрические зависимости

Различают геометрические и размерные зависимости. Геометрические зависимости управляют взаимным положением объектов. Будучи приложенными к объектам, они приводят объекты в требуемое положение и поддерживают его при перемещении или вращении объектов.

Для присвоения геометрической зависимости следует указать кнопку зависимости в панели (см. рис. 26.2, а) и указать объекты, к которым зависимость прикладывается. Рассмотрим пример (рис. 26.3) приложения геометрических зависимостей, приводящий к преобразованию произвольного четырехугольника в квадрат:

? line (Отрезок) / постройте произвольный четырехугольник (рис. 26.3, а).

Для того чтобы контур, составленный из отрезков, был замкнутым и представлял единое целое, присвоим конечным точкам отрезков зависимость совпадения:

• ? на инструментальной панели (см. рис. 26.2, а) найдите кнопку геометрической зависимости совпадения (поз. 1). Установив на нее курсор, прочтите краткую информации о применении этой зависимости;
• ? укажите кнопку зависимости совпадения. В командной строке прочтите требуемые действия по выполнению команды и укажите какую-либо пару отрезков вблизи точки их совмещения. В точке совмещения возник значок совпадения — квадратик (поз. У, см. рис. 26.3, а)

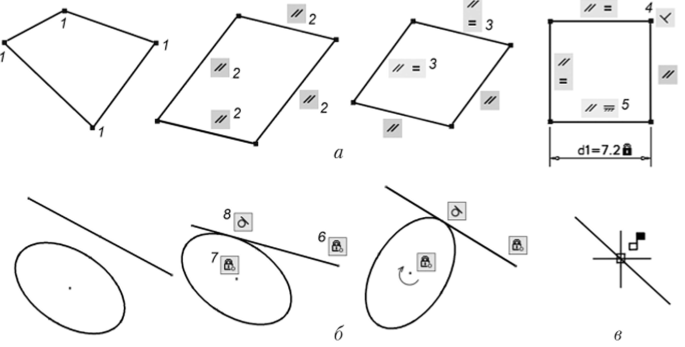
Рис. 26.3. Примеры геометрических зависимостей

• ? повторите совмещение для оставшихся вершин контура — значки совпадения возникли во всех вершинах;
• ? укажите одну или несколько сторон контура — возникли ручки. Потянув за какую-либо ручку, убедитесь, что при деформировании контур остается замкнутым.

Введение

м геометрических зависимостей последовательно преобразуем четырехугольник в параллелограмм, ромб, квадрат (см. рис. 26.3, а):

• ? укажите кнопку зависимости параллельности и две противоположные стороны четырехугольника — стороны стали параллельны (образовалась трапеция), рядом с каждой из указанных сторон возник значок параллельности (поз. 2, рис. 26.3);
• ? присвойте параллельность второй паре противоположных сторон — образовался параллелограмм;
• ? укажите одну из вершин и потяните возникшую ручку — при деформировании контура сохраняется параллелограмм;
• ? присвойте паре смежных сторон зависимость равенства длины — рядом с указанными сторонами возникли значки равенства (ноз. см. рис. 26.3), образовался ромб;
• ? присвойте паре смежных сторон зависимость перпендикулярности (поз. 4, см. рис. 26.3) — образовался квадрат; указав его стороны, потяните за ручки — квадрат сохраняется;

U присвойте одной из сторон свойство горизонтальности (поз. 5, см. рис. 26.3) — квадрат принял конечное положение.

В качестве второго примера рассмотрим геометрические зависимости касания и фиксации.

? постройте эллипс и отрезок прямой линии (см. рис. 26.3, б).

Ограничим перемещение объектов, приложив к ним зависимость фиксации.

Фиксировать можно либо точку объекта, либо весь объект. В нашем примере зафиксируем конечную точку отрезка и центр эллипса:

• ? укажите знак фиксации («замок» поз. 2, см. рис. 26.2. а) и правую конечную точку отрезка — рядом с отрезком возник знак фиксации (поз. 6);
• ? укажите эллипс — в центре эллипса возник знак фиксации эллипса (поз. 7);
• ? присвойте зависимость касания отрезка и эллипса (поз 3, см. рис. 26.2) — объекты приведены в положения касания. Возник значок касания (поз. 8);

? вращайте (команда rotate) эллипс вокруг его центра — при вращении сохраняется касание отрезка и эллипса. Получена модель кулачкового механизма.