Твердое состояние. 
Решение обратной задачи стабильности

В качестве критерия устойчивости состояний окисления в твердых соединениях целесообразно принять величины энергии Гиббса перехода, которому отвечает изменение состояния окисления центрального атома комплекса. Здесь возможно, по меньшей мере, два подхода.

Первый подход заключается в использовании представлений об энергии решетки^[1]. Так, например, расчетом по циклу Борна — Габера можно получить формулу, характеризующую устойчивость ML, к разложению до ML"__t с отщеплением «одновалентного» лиганда L. Она выглядит следующим образом:

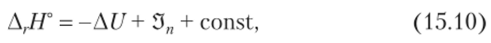
где ДU — разность энергий решетки ML, и ML"__t, 3″ — потенциал ионизации, const — сумма энтальпий атомизации и сродства к электрону лиганда. Использование такого рода уравнений выгодно, когда можно пренебречь энтропийным членом, например, при анализе изменений параметров термодинамической устойчивости в каком-то ряду, при условии, что изменение энтропии в нем будет либо постоянной величиной для всех членов ряда, либо изменяться в том же ряду монотонно и известным образом.

Величины Д (но Лёвдину) зависят от геометрии, способности к деформации «разновалентных» ионов, от обменных членов энергии решетки и членов, зависящих от перекрывания орбиталей (безусловно на ДU накладывают отпечатки изменения «маделунговского» потенциала^[2]).

Значения А[7_реш удобно оценивать с помощью эмпирических соотношений. К примеру, для расчета энтальпий перехода ?п?_А в ЬпЕ₃ воспользовались оригинальным приемом. Было замечено, что соотношение средних межъядерных расстояний Ьп—Б в ?п?_А и ЬпБ₃ оказывается постоянной величиной, тогда А[7_рсш можно записать в виде двучлена.

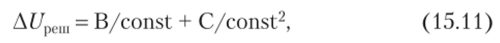
являющегося по сути аналогом уравнения Борна — Майера (см. уравнение (3.2)). В (15.11) константы В и С легко определяются по крайней мере, но двум реперным точкам редкоземельного ряда, удаленным в этом ряду по возможности максимально друг от друга. Надежность расчета (и делающихся из него выводов) зависит лишь от точности упомянутых реперных значений и существенно выше, чем нахождение разности энергий решетки МР^ и МР₃, рассчитанных, например, по стандартным термохимическим циклам, что отягощено значительными погрешностями.

Второй подход заключается в том, что энергии химических процессов (?), например диссоциации, представляют в виде разностей аддитивных членов уравнения Татевского (см. параграф 3.10). Может показаться, что такого рода энергии являются весьма грубой оценкой, а сам подход является следствием предыдущего. Однако это не совсем так.

Действительно, аддитивное представление энергии в виде суммы так называемых парциальных энергий является самостоятельным методическим приемом и основывается на глубоких теоретических обобщениях. Прежде всего, такой подход базируется на постулате о возможности аддитивного разложения макроскопической характеристики вещества, например, внутренней энергии на вклады эффективных атомов и эффективных связей:

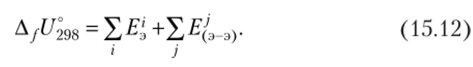
Этот постулат не противоречит квантово-химическим моделям строения вещества. Это наиболее простое и наглядное уравнение получено Яровым (1978) для органических соединений. Более подробный анализ только лишь уточняет картину, но не входит в противоречие с выводами, полученными при элементарном рассмотрении.

Опробование метода на большом числе органических соединений, для которых характерно явление гомологии, используемое для нахождения парциальных вкладов уравнения (15.12), показывает, что вклады эффективных связей в общую величину А/11^ могут быть учтены введением поправок в инкременты, оиределяемыс только для эффективных атомов. При этом уравнение (15.12) принимает следующий вид:

Для неорганических объектов применение аддитивной схемы (15.12), как и схемы (15.13), (см. также параграф 3.10) существенно затруднено отсутствием явления гомологии, необходимого для строгого решения системы уравнений, включающей величины Е^[3]Э аддитивного уравнения.

В то же время достаточно надежные значения энергии или энтальпии образования по крайней мере газообразных галогенидов и оксидов оказалось возможным получить при рассмотрении корреляций вида.

где параметр Н_М(_П) задается уравнением.

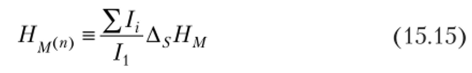
где /, — потенциалы ступенчатой ионизации; А₅Н_М — энтальпия сублимации металла (= А/Н°_м).

Упомянутая зависимость А^Я^МХ, от Н (_Я> аналогична использованным в работе Ярового^[3]. Из этого следует, что энергетика «изосоставных» соединений (бинарных и комплексных) прямо зависит (внутри указанных выше групп соединений) от параметров, характеризующих род эффективных атомов, т. е. химической индивидуальности и валентности (термины классической теории химического строения). Для таких соединений энергетические параметры рода (или состояний окисления) прямо коррелируют с энтальпиями образования, так как типовые и видовые характеристики элементов в «изосоставных» рядах близки.

Из изложенного следует, что вывод относительно строгого и термодинамически обоснованного суждения об устойчивости состояний окисления возможен, если проводится сопоставление рядов соединений, содержащих элемент в одинаковых состояниях окисления, а сами ряды характеризуются близкими типовыми и видовыми параметрами. Пример подобного анализа для производных М^ш и М^1У (М = Ьп, Ап) дается в работе Ю. М. Киселева^[5] (1986).

Рассмотренные критерии стабильности состояний окисления позволяют заметить, что анализ величин изменений энергий Гиббса в рядах однотипных процессов, которым можно поставить в соответствие переход одной валентной формы к другой, позволяет судить об изменении их стабильности в тех же рядах. Процедура постановки в соответствие величины Д_ГС° параметрам, характеризующим валентные переходы, при решении обратной задачи, конечно, феноменологическая. Это, однако, не означает, что аналогии здесь являются единственно возможным приемом. В ряде случаев при анализе однородных объектов и соответствующих «валентных» переходов удается выявить характерные факторы и обосновать собственно процедуру.

Известны и иные способы оценки стабильности состояний окисления, базирующиеся, например, на установлении корреляций между характеристиками соответствующих ионов и наблюдаемыми фактами. Так, Л. Аренс в начале 1950;х гг. прослеживал соотношения между потенциалами ионизации и известными состояниями окисления элементов и сделал вывод, что при ДЗ М" ^-1 и М" ~² в интервале 1200—2400 кДж состояния окисления М" ^-1 и М" могут быть стабилизированы; если эти разности больше -2400 кДж, то более высокое состояние окисления не достигается химическими методами. Согласно этой работе, можно ожидать достижения состояний Ш)(П), С8(П), 2п (Ш), Сс1(Ш), Н§(Ш), которые в свое время многие химики пытались реализовать, правда, безуспешно. Отметим, что имеются весьма веские энергетические аргументы в пользу невозможности реализации производных 7п (1П), Сс1(Ш) [Каирр М., е1 а1. 1994].

Таким образом рассмотренные общие принципы создают предпосылки для корректного анализа окислительно-восстановительных процессов, позволяют судить о возможности их реализации, а также проводить надежные оценки. Отметим, что общие подходы для молекулярных, газообразных галогенидов и оксидов ограничены из-за отсутствия достаточного числа надежных термодинамических данных. Поэтому для решения задач о стабильности бинарных и, в особенности, комплексных соединений большое значение приобретают взгляды, основанные на идее о факторах, способствующих и препятствующих стабилизации состояний окисления, подоплекой которой остается принцип аддитивности энергий и энтальпий.

• [1] Круговые циклы типа цикла Борна — Габера или Фаянса исходят из представлений об энергии решетки, причем эта энергия для растворных систем при О Кпрямо является энергией Гиббса.
• [2] Madelung part of lattice energy — MAPLE. Интересно, что суммы MAPLEбинарных соединений AB и ВС, «составляющих» тройное соединение АВС, практически равны MAPLE тройных соединений АВС (Хоппе Р., 1978).
• [3] Яровой С. С. Методы расчета физико-химических свойств углеводородов.М.: Химия, 1978.
• [4] Яровой С. С. Методы расчета физико-химических свойств углеводородов.М.: Химия, 1978.
• [5] Киселев Ю. М. Термодинамика стабилизации состоянии окисления металлов в твердых телах. Анализ энтальпий образования бинарных галогенидов, оксидов и некоторых комплексных галогенидов / Москва, 1986; деп. в ВИНИТИ№ 8903−2/86.