Задачи линейного программирования

Задача нахождения экстремального значения линейного функционала на множестве, определяемом системой линейных ограничений в виде равенств или неравенств, называется задачей линейного программирования.

Задача линейного программирования может быть сформулирована, например, следующим образом. Найти.

при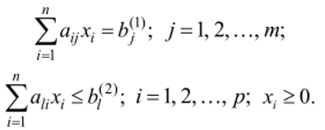

Здесь c_i — весовые коэффициенты линейной целевой функции; Ь^

bj²⁾ — заданные значения ограничений.

Иными словами, задача линейного программирования состоит в том, что необходимо найти такие неотрицательные значения переменных x_j9 которые, удовлетворяя системе линейных уравнений и (или) неравенств, обращали бы в максимум линейную целевую функцию. Для простоты предположим вначале, что отсутствуют ограничения в форме неравенств. Тогда задача линейного программирования может быть представлена в виде:

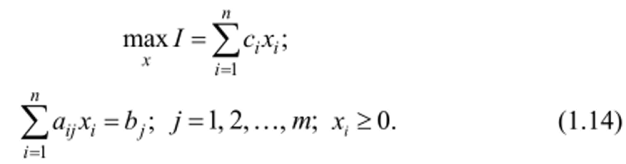
Необходимое условие существования оптимального решения в задачах линейного программирования связано с наличием системы ограничений. Из (1.14) видно, что при отсутствии ограничений оптимального решения нс существует, т. к. значения переменных и целевой функции могут быть бесконечными.

Как уже отмечалось ранее, система линейных ограничений задает допустимое множество значений х_г Поэтому для обсуждения возможных решений задачи линейного программирования необходима система линейных ограничений, которые в данном случае заданы в виде равенств. Допустимые значения х₍ могут быть получены из решения этой системы.

Систему линейных уравнений, обладающую решениями, называют совместной. Как известно из линейной алгебры, существует несколько возможных исходов в решении совместной системы уравнений.

Вначале положим, что число неизвестных п равно числу уравнений т₉ т. е. т = я, а уравнения линейно независимы. Если система уравнений совместна, то она является определенной и обладает одним-единственным решением. В этом случае задача оптимизации теряет смысл.

Рассмотрим теперь случай, когда число линейно независимых уравнений меньше числа неизвестных, т. с. т < п. Если система уравнений совместна, то у нее существует бесчисленное множество решений. При этом любым переменным п — т можно придавать любые значения. Такие переменные называются свободными. Остальные переменные выражаются через свободные и называются базисными.

Случай, когда число линейно независимых уравнений больше числа неизвестных, требует иных методов решения и здесь не рассматривается. В задачах линейного программирования основной является ситуация, когда число линейно независимых уравнений меньше числа неизвестных и существуют различные решения, среди которых необходимо выбрать оптимальное.

Дадим задаче линейного программирования геометрическую интерпретацию. Для этого положим, что число линейно независимых уравнений на два меньше числа независимых переменных, т. е. п — т = 2.

Тогда, выбрав любые две переменные, например х_] и х₂, в качестве свободных, выразим через них остальные т базисных.

(По условию Xj должны быть неотрицательными.) Выбрав значения д:_; =0, получим т — п — 2 уравнений прямых, которые на плоскости и х₂ составят область допустимых решений, последняя на рис. 1.19 выделена штриховкой.

Найдем теперь оптимальное решение из числа допустимых. Применяя уравнение (1.15), выразим целевую функцию через свободные переменные х₁ и х₂. В результате получим

Найдем такие л, и х₂, при которых целевая функция достигает оптимального значения. Придавая целевой функции различные, но постоянные значения, получим линии равного уровня в виде параллельных прямых на плоскости jCjOjc^, рис. 1.17.

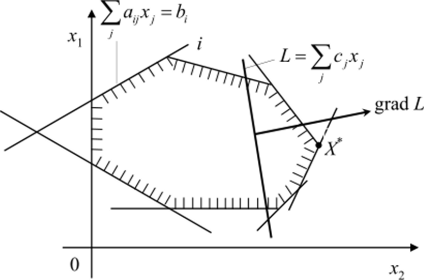
Рис. 1.19. Геометрическая интерпретация задачи линейного программирования

Пусть при перемещении прямой, характеризующей целевую функцию, в направлении, указанном стрелкой, целевая функция будет возрастать.

Очевидно, что максимального значения из всех допустимых целевая функция достигает в наиболее удаленной точке X* с координатами х*, х. Эта точка представляет собой вершину многоугольника ограничений. Подставляя в уравнение (1.15) значения х,*, х*₂, можно найти оптимальные значения базисных переменных, а из уравнения (1.16) — оптимальное значение целевой функции.

Пусть теперь ограничения задаются не уравнениями, а неравенствами. Можно заметить, что неравенства могут быть сведены к уравнениям, если ввести дополнительные переменные:

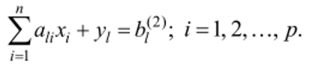
Таким образом, задача линейного программирования с ограничениями в форме неравенств может быть сведена к задаче линейного программирования с ограничениями в форме уравнений за счет увеличения числа переменных.

Перечислим теперь некоторые особенности, относящиеся к задаче линейного программирования.

• 1. Для того чтобы существовало оптимальное решение, целевая функция должна быть задана на замкнутом ограниченном множестве.
• 2. Число линейно независимых уравнений, которые задают множество ограничений, должно быть меньше числа неизвестных.
• 3. Решение задачи линейного программирования, оптимизирующее целевую функцию, всегда достигается в вершине многоугольника ограничений.
• 4. Решение является единственным, если линия равного уровня целевой функции нс параллельна линиям ограничений в той стороне, где достигается оптимум. В противном случае задача имеет бесчисленное множество оптимальных решений.
• 5. Для того чтобы найти оптимальное решение, достаточно перебрать вершины и выбрать из них ту, где функция достигает оптимального значения.

Все перечисленные особенности сохраняются и в том случае, когда число неизвестных превышает число независимых уравнений больше чем на два. Только теперь множество, заданное ограничениями, в пространстве свободных переменных представляет собой выпуклый многогранник.

Прямой перебор вершин выпуклого многогранника даже при небольшом числе переменных и линейно независимых решений является трудоемким и малоэффективным способом решения задачи линейного программирования. Поэтому для решения подобных задач разработаны и разрабатываются алгоритмы направленного поиска оптимального решения. В основе всех современных вычислительных алгоритмов широко используется направленный поиск оптимального решения, известный под названием симплекс-метода. В этом методе решение задачи распадается на два этапа:

1) отыскание координат первой вершины многогранника ограничений, или (в терминах линейного программирования) опорного плана;

2) отыскание координат вершины многогранника ограничений, соответствующего оптимальному значению целевой функции (оптимального плана).

Процедура отыскания координат оптимальной вершины в симплекс-методе предполагает проверку координат вершины (плана) на оптимальность и переход в ту из соседних вершин, для которой значение целевой функции ближе всего подходит к оптимальному.

Таким образом, вычисление в симплекс-методе ведется по следующей схеме.

На первом этапе находится какое-нибудь, хотя бы и не очень удачное решение, удовлетворяющее совокупности линейных ограничений, или устанавливается, что такого решения не существует. На этом этапе выбираются базисные переменные, которые затем выражаются через свободные. Значения целевой функции выражаются через свободные переменные.

На следующем этапе выбирается та из свободных переменных, введение которой в число базисных способно улучшить значение целевой функции. Определяется, какая из базисных переменных должна быть исключена и сделана свободной. Геометрически эти операции эквивалентны выбору того из ребер многогранника ограничений, соединяющих исходную вершину с соседними, проекция градиента целевой функции на который максимальна. Затем вновь вводимая базисная переменная выражается через переменную, выводимую из числа базисных, и другие свободные переменные. Все остальные базисные переменные и значения целевой функции выражаются через новые свободные переменные. Если окажется, что введение любой из свободных переменных неспособно улучшить значение целевой функции, то найденная вершина является оптимальной. В противном случае все операции второго этапа повторяются. Доказано, что, если следовать этой схеме, оптимальное решение будет получено через конечное число шагов.

Рассмотрим некоторые из формальных методов, связанных с выбором опорного плана и способов его улучшения.

Пусть задача линейного программирования сформулирована следующим образом: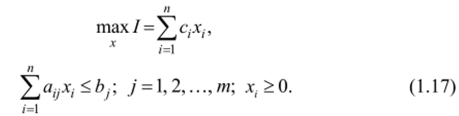

Если все компоненты Ъ. неотрицательны, то первый опорный план уже найден и определяется значениями х, =0; / = 1,2,./?. Если среди bj есть к отрицательных, это значит, что решение нс является опорным и его предстоит найти. Для отыскания первого опорного плана необходимо производить обмен базисных и свободных переменных так, чтобы число отрицательных свободных членов b. (j = 1,2,…,к) с каждым этапом перебора убывало. Если в результате просмотра всех свободных переменных среди свободных членов останутся отрицательные, то система уравнений является несовместимой и допустимых решений не имеет.

Пусть теперь первый опорный план найден. Существует ряд методов проверки координат вершины на оптимальность. Остановимся на одном из них. Задача линейного программирования уже сформулирована в виде (1.17). Назовем такую задачу прямой. С нею связывается другая, которая по отношению к прямой называется двойственной:

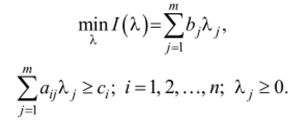
Из теоремы о соотношении прямой и двойственной задач, которая доказывается в линейном программировании, следует, что если существует решение прямой X* (/ = 1,2,…,п) и двойственной Л* (j = 1,2,…,т) задачи, то справедливо соотношение.

где s — множество индексов тех ограничений двойственной задачи, которые выполняются как строгие равенства в точке X_t (/ = 1,2,…, п).

Доказывается, что если.

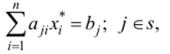
то х* является оптимальным решением прямой задачи в том и только в том случае, если существуют такие А,_; > 0, при которых.

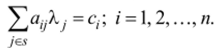
Таким образом, для исходной вершины решается двойственная задача (разыскивается XX Если вершина не оптимальна (нс все Xj > 0), то из исходного множества $ выводится некоторый элемент к, определяемый по правилу.

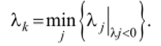
Геометрически это соответствует движению по ребру в сторону максимального улучшения значения целевой функции.