Спектральные закономерности. 
Дискретность динамических переменных классической физики

Как уже отмечалось в гл. 1, атомистическая теория возродилась на научной основе в XIX веке благодаря Дж. Дальтону, принявшему, однако, неверную точку зрения (восходящую еще к философу Демокриту, не имевшему никакого понятия о химических элементах и их атомах) на неделимость атомов. В XIX веке эта неверная демокрито-далыоновская точка зрения критически осмыслена не была и превратилась, по-существу, в догму. II хотя эпизодически производились попытки дать объяснение природы линейчатых спектров испускания и поглощения, в рамках догматических взглядов на неделимость атомов химических элементов понять происхождение спектров было невозможно, гак как спектры обуславливаются внутриатомными процессами, к тому же описываемыми вовсе не законами классической физики.

Поэтому прогресс в области спектроскопии на протяжении XIX века был связан лишь с совершенствованием экспериментальной техники. Тем не менее, и прогресс чисто эмпирической спектроскопии принес плоды, позволив открыть важный закон природы — комбинационный принцип, сыгравший большую роль при выработке новых квантовых законов, описывающих поведение вещества на микроуровне.

В связи с прогрессом в области спектроскопии упомянем лишь шведского ученого Ангстрема (именем которого была названа единица длины, широко используемая в атомной физике), достигшего при измерении длин волн спектральных линий абсолютной точности как раз примерно в 1 А. Ангстрем изучал спектры пламени, дуги, Солнца, планет, обнаружил в 1862 году водород на Солнце; в 18G8 году составил атлас, содержащий описание более 1 000 фраунгоферовых линий, сравненных с линиями спектров испускания земных элементов. В частности, Ангстрем изучил самый простой из всех спектров — спектр испускания атомарного водорода, состоящий всего из четырех линий в видимой части. Эти четыре линии получили обозначение Н_а (красная), Нр (синяя), Н_у и Н$ (две фиолетовых линии). Экспериментально определенные Ангстремом длины волн этих линий получились равными G5G2.10, 48G0.74, 4340.10 и 4101.20 А.

Швейцарский математик и физик Бальмер в 1885 году подобрал формулу, описывающую длины волн видимой части водородного спектра испускания с высокой точностью:

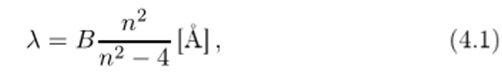
где В = 3645.6, а целое число п = 3,4,5,6.

В самом деле, если вычислить длины волн по формуле Бальмера (4.1), то получим, соответственно, G5G2.08, 4860.80, 4340.00 и 4101.30 [А]. Максимальная разница между значениями длин волн, определенными Ангстремом, и значениями длин волн, вычисленными по формуле Бальмера, не превышает ±0.1 А, что лежит в границах погрешности измерений Ангстрема.

Рис. 4.G. Серия Бальмера спектра испускания атомарного водорода.

Бели в формулу Бальмера подставить п = 7,8,9,10,11, то получатся длины волн, лежащих в ближнем ультрафиолете^[1] и наблюдавши хся эксперим ентально.

Все линии спектра испускания водорода, описываемые фо!>- мулой Бальмера (4.1), получили название серии Бальмера.

На рис. 4.6 изображен фрагмент спектра испускания водорода в видимой и ближней ультрафиолетовой частях, на котором отчетливо видны первые 11 линий серии Бальмера. Интенсивность линий при п > 10 быстро слабеет, и они не видны на рисунке. При п +оо получается граничная длина волны, за которой линейчатый спектр испускания переходит в сплошной.

Формулу Бальмера можно преобразовать, если ввести в рассмотрение вместо длины волны частоту линии v = с/А. Тогда (4.1) можно записать в виде разности двух членов:

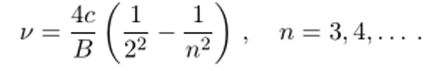
Поскольку скорость света в XIX веке была определена с относительно невысокой точностью, постольку спектроскописты стали пользоваться не частотой линии, а обратной длиной волны, получившей специальное обозначение^[2] V и зачастую не совсем верно называемой волновым числом (волновое число к есть 2п/Х = 2я17). Пользуясь обратной длиной волны, формулу Бальмера (4.1) можно привести к виду.

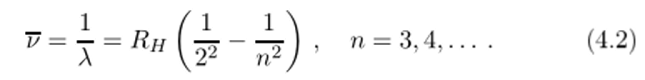
где постоянная 4/В (обозначенная как Яц) мало отличается^[3] от постоянной Ридберга R, современное значение которой.

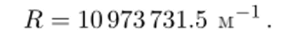
Как это следует из табл. 4.2, спектры испускания щелочных металлов принадлежат к простейшим (после водорода), хотя и содержат огромное число линий. Спектроскописты (уже до Ридберга) сумели разглядеть некоторый порядок в кажущемся хаосе сотен линий спектров испускания щелочных металлов, разделив все линии на серии, которые были названы резкой, гласной, диффузной и фундаментальной.

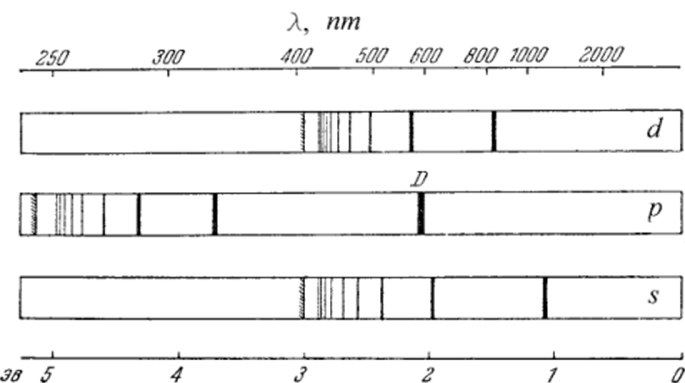
Рис. 4.7. Диффузная (d), главная (/?) и резкая (s) серии Na.

Так, на рис. 4.7 единый спектр натрия разбит на три важнейшие серии, изображенные схематично, чтобы дать общее представление о спектре излучения натрия.

Сверху дана шкала длин воли, а снизу — энергий испускаемых фотонов.

Спектроскопические исследования показали, что линии диффузной (diffuse, англ.) серии являются триплетами, которые при недостаточном разрешении спектрометра сливаются в одну размытую линию, что и дало название серии.

Следующая серия начинается с наиболее яркой линии испускания натрия — знаменитого дублета D. По понятной причине эта серия получила название главной (principal, англ.). Оказалось, что все линии главной серии — дублеты, расстояние между' линиями которых уменьшается по мере уменьшения длины волны.

Наконец, последняя серия — резкая (sharp, англ.) — также состоит из дублетов, расстояние между которыми, однако, постоянно, а сами линии дублетов относительно других серий резкие.

Так же, как и серия Бальмера для водорода, серии натрия имеют граничные длины волн, после которых спектр переходит в непрерывный. Существует и еще одна серия в спектре испускания — фундаментальная (fundamental, англ.). Однако она более слабая и не показана на рисунке.

Аналогичен вид спектров испускания и для остальных щелочных металлов. Ридберг поставил перед собой цель найти эмпирические выражения для длин волн серий испускания щелочных металлов, аналогичные формуле Бальмера для водорода, и в 1900 году нашел, что серии неплохо описываются выражениями.

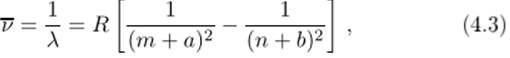
где а и b — константы, определяемые конкретной серией; га = 1 для главной серии, га = 2 для резкой и диффузной серий, га = 3 для фундаментальной серии; п — целое число (параметр линии, причем п > га); наконец, R — единая для всех серий константа. Например, главная серия спектра испускания натрия хорошо описывается выражением.

где целое число п = 2,3,4…. Формула Батьмера в форме (4.2), очевидно, является частным случаем формулы Ридберга (4.3).

В и без того неясный вопрос о происхождении спектров Ридберг внес глубоко интригующее обстоятельство, заключающееся в том, что спектры разных элементов определяются общей константой R (постоянной Ридберга).

Размышляя над результатами Ридберга, швейцарский математик и физик-теоретик Ритц решил, что формулы (4.3) и (4.2) содержат разности не случайно, и что, например, формулу для серии Бальмера (4.2) можно записать в виде разности двух величин, которые Ритц назвал спектральными термами, или просто термами Т (п):

где для атома водорода.

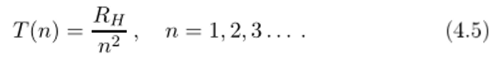
Почему в последней формуле п начинается с единицы (а не с двойки), разъясняется далее.

В 1908 году Ритц^[4], изучая спектры различных элементов, сформулировал комбинационный принцип, оказавшийся точным законом природа^[5]. В частности, рассматривая двухчленные сериальные формулы Ридберга, Ритц пришел к следующим выводам:

«Видно, что:

• 1°. Простые законы относятся всегда к 1/А, то есть к частоте.
• 2°. При бесконечном увеличении одного из целых чисел получаемые частоты стремятся к пределу.
• 3°. Каждый из двух членов формулы до некоторой степени независим и линии спектра получают, комбинируя между собой такие члены различными способами".

Другими словами, комбинационный принцип можно сформулировать следующим образом:

Каждому изотопу можно сопоставить такую последовательность термов Т (п), что все линии спектра испускания изотопа могут быть получены как разности двух каких-либо термов: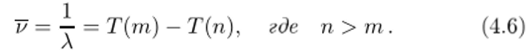

Ритц предложил нумеровать термы так, чтобы они образовывали убывающую последовательность положительных чисел. Если зафиксировать целое число т, определяющее первый терм в (4.6), и придавать п возрастающие значения, то из всего спектра выделяется определенная спектральная серия. Например, выше были продемонстрированы главная, диффузная и резкая серии в спектрах щелочных металлов.

Из комбинационного принципа легко вывовести следствие, которое позволяет проверить правильность этого принципа па примере спектра любого элемента независимо от того, известны или нет выражения, описывающие его термы.

Покажем, что из комбинационного принципа следует, что разность волновых чисел двух спектральных линий одной серии может быть также возможным волновым числом, принадлежащим другой серии.

Пусть Т7_пт = Т (п) — Т (тп) н v"(_m+k) = Т (п) — Т (тп + к).

Тогда имеем V_{n (rn+k)} — ~_nm = T (m) — Т (тп + к) = ~_{m (m}+k) —

Таким образом, если выделить в спектре элемента спектральную серию, то разности двух любых волновых чисел дадут возможное^[6] волновое число спектра, что можно проверить.

Надо сказать, что вначале комбинационный принцип был воспринят как числовой курьез из области спектроскопии, а не как закон природы, имеющий фундаментальное значение. Тем не менее, на основе комбинационного принципа Ритц в 1908 году предсказал новую серию в спектре испускания водорода.

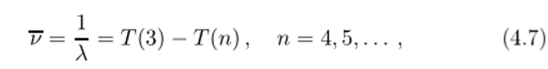
которая в том же году была открыта в инфракрасной области немецким физиком Пашеном.

Как видно, Ритц не поддался искушению предсказать линии в спектре водорода, отвечающие т = 1,4,5,…, хотя это и следовало из его же комбинационного принципа. Подобное предсказание сделал только в 1913 году Нильс Бор, исходящий уже из ясного представления о происхождении спектров. II действительно, в 1914 году американский физик Л&йман впервые щюизвел измерения в области вакуумного ультафиолета (что потребовало разработки новой техники), открыв новую серию в спектре испускания водорода, представляемую выражением.

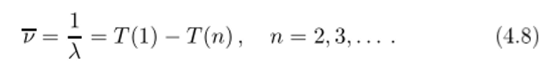
Серия в далекой инфракрасной области в спектре испускания водорода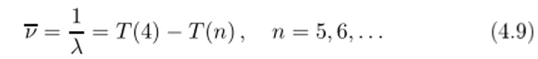

была открыта только в 1922 году (из-за технических сложностей работы в далекой инфракрасной области) американским физиком Брэкетом, а серия.

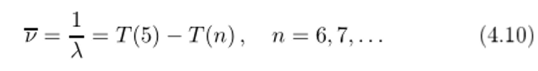
в еще более далекой инфракрасной области была открыта в 1921 году американским физиком Пфундом.

Другими словами, обобщенное выражение для спектральных линий испускания водорода с учетом всех обнаруженных серий принимает вид.

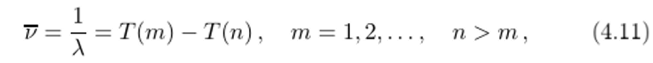
где выражение для термов водорода имеет вид (4.5).

Итак, к началу XX века наивысшим достижением спектроскопии (помимо высокоразвитой техники измерений и накопления огромного эмпирического материала) стал комбинационный принцип, сформулированный Ритцем. По мере повышения экспериментальной точности измерений длин волн комбинационный принцип подтверждался снова и снова. Однако, как уже отмечалось, этот принцип рассматривался, скорее, как некий числовой курьез, а не как общий закон природы. Даже сам автор принципа, Ритц, как мы видели на примере предсказания новых серий для спектра испускания водорода, не воспользовался вытекающими из принципа следствиями.

Проблема заключалась в том, что после открытия электрона в 1897 году, когда, наконец, стало ясно, что атом делим, что атом имеет структуру, и что испускание и поглощение излучения вызываются внутриатомными процессами (то есть движением электронов в атоме), классическая физика стала предсказывать, что частоты линий испускания атома должны определяться частотами периодических движений электронов в атоме.

Но если электрон в атоме будет каким-либо образом двигаться с частотой is и при этом испускать излучение, то амплитуда этого излучения, фиксируемая в любой точке пространства, будет непременно периодической функцией времени, а спектр периодической функции, определяемый ее разложением в ряд Фурье, дискретен и содержит только целые кратные основной частоты I/, что резко противоречит комбинационному принципу!

Предсказание же классической физики в равной мере относилось и к модели атома Томсона (в которой электроны колебались вокруг положения равновесия), и к ядерной модели атома Резерфорда (в которой электроны вращались вокруг ядра), сменившей модель Томсона, поскольку в рамках последней оказалось невозможным объяснение результатов рассеяния rv-частиц фбльгами (см. гл. 2, подраздел 2.9.2).

Кроме того, излучающий электрон должен терять кинетическую энергию, что ведет к коллапсу атома в рамках резерфо!>- довской модели (см. подраздел 2.9.G гл. 2), если считать, что законы классической физики описывают поведение электронов в атоме, что, разумеется, также противоречит наблюдаемой устойчивости окружающего мира.

Таким образом, первая же попытка объяснить происхождение спектров на основе классических представлений, последовавшая за открытием делимости атома, вступила в противоречие с громадным эмпирическим спектроскопическим материалом и комбинационным принципом.

Путь к выход}' из тупика сумел найти двадцативосьмилетний датский физик Нильс Бор, который решился частично порвать с классическими представлениями, чтобы развить ядерную модель атома Резерфорда (на примере простейшего атома водорода, состоящего из ядра и одного электрона) с целью, во-первых, объяснить устойчивость атома (то есть отсутствие постоянных потерь энергии па излучение) и, во-вторых, объяснить происхождение линейчатых спектров испускания и поглощения.

• [1] Характсрной чертой ультрафиолетового излучения является рост егопоглощения веществом по мерс уменьшения длины волны. Так, обычноестекло перестает пропускать излучение с Л = 3200 А, а воздух (из-за поглощения кислородом) — с Л = 1850 А. Последняя длина волны и делитультрафиолетовый диапазон на ближний и дальний (или вакуумный).
• [2] Обычным делом в спектроскопии было обозначение обратной длиныволны просто буквой г/, что совпадает с обозначением частоты. К сожалению, подобная практика перекочевала в некоторые учебники, но атомной физике, что, несомненно, сбивает не слишком внимательных читателей с толку.
• [3] Далее разница между постоянной Ридберга для водорода Ян и постоянной Ридберга R будет разъяснена (см. стр. 227).
• [4] ‘‘Вальтер Ритц умер в 1909 году, прожив всего 31 год.
• [5] Иногда комбинационный принцип, или принцип Ритца, называют такжепринципом Ридберга-Ритца.
• [6] 4Правда, в силу существования правил запрета, о которых будет идтиречь далее, вычисленное таким образом волновое число может в реальномспектре не наблюдаться.