Теорема Гаусса в дифференциальной форме

Теорема Гаусса в интегральной форме выражает связь между потоком вектора D через поверхность S, ограничивающую некоторый объем, и алгебраической суммой зарядов, находящихся внутри этого объема. С помощью теоремы Гаусса в интегральной форме нельзя определить, как связан исток линий D в данной точке поля с плотностью свободных зарядов в этой же точке поля. Ответ на этот вопрос дает дифференциальная… Читать ещё >
Теорема Гаусса в дифференциальной форме (реферат, курсовая, диплом, контрольная)
Теорема Гаусса в интегральной форме выражает связь между потоком вектора D через поверхность S, ограничивающую некоторый объем, и алгебраической суммой зарядов, находящихся внутри этого объема. С помощью теоремы Гаусса в интегральной форме нельзя определить, как связан исток линий D в данной точке поля с плотностью свободных зарядов в этой же точке поля. Ответ на этот вопрос дает дифференциальная форма записи теоремы Гаусса. Чтобы прийти к ней, разделим обе части уравнения (19.16) на одну и ту же скалярную величину — на объем V, находящийся внутри замкнутой поверхности S:

'> Имеется в виду вектор, изображающий элемент поверхности сферы.
Выражение (а) остается справедливым для объема V любой величины. Устремим объем к нулю:
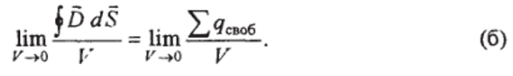
При стремлении объема к нулю ^5 dS также стремится к нулю, но отношение двух бесконечно малых величин ?3 dS и V есть величина конечная?>. Предел отношения потока векторной величины сквозь замкнутую поверхность, ограничивающую некоторый объем, к объему V называют дивергенцией вектора 5 (divD). Часто вместо термина «дивергенция» употребляют термин «расхождение» или «исток» вектора 5.
В правой части выражения (б) находится объемная плотность свободного заряда рсво6.
Таким образом, теорему Гаусса в дифференциальной форме записывают следующим образом (первая форма записи):

т. е. исток линий D в данной точке поля определяется значением плотности свободных зарядов в этой точке. Если объемная плотность зарядов в данной точке положительна (рсвоб > 0), то из бесконечно малого объема, окружающего данную точку поля, линии вектора D исходят (исток положителен, рис. 19.8, а). Если в данной точке поля <0, то в.
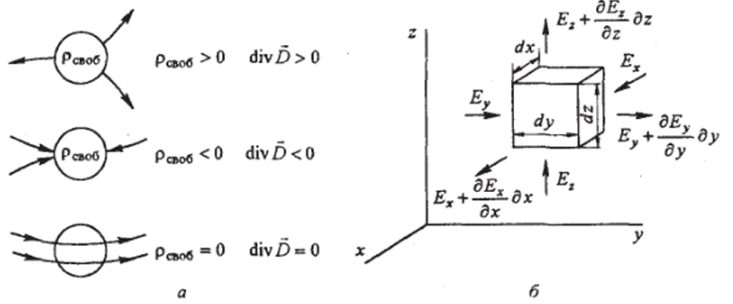
Рис. 19.8.
бесконечно малый объем, внутри которого находится данная точка, линии вектора 5 входят. И, наконец, если в какой-либо точке поля Рс"об = 0, то в данной точке объема нет ни истока, ни стока линий D, т. е. в данной точке линии вектора D не начинаются и не заканчиваются.
** В III ч. учебника неоднократно использованы величины, которые определяются при стремлении рассматриваемого объема или площади к нулю. Стремление к нулю не следует понимать дословно, речь идет о таком уменьшении линейных размеров объема или площади, при котором еще не сказывается дискретность материи.
Если среда однородна и изотропна, то ее е, = const. Вместо (19.20) запишем выражение div sa Ё = рсоо6.
Вынесем sa за знак дивергенции:
следовательно,.

Формула (19.21) представляет собой вторую форму записи теоремы Гаусса. Она справедлива только для однородной и изотропной сред. Для неоднородной среды с, является функцией координат, и потому она не может быть вынесена за знак дивергенции.
Уравнение (19.17а) в дифференциальной форме записывают так (третья форма записи):
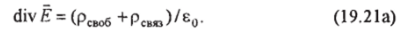
Следовательно, истоком вектора Е, в отличие от истока вектора D. являются не только свободные, но и связанные заряды.
В различных системах координат div Ё раскрывается по-разному.