Пути в графе, связность

В графе Г путем из вершины / в вершину j (соединяющим вершины / и j) называется система ребер или дуг: s_{; /} = {(/₀, /_t), (/_1? /₂), (//_], //)}, где /₀ = /, // = j_f вершины пути / и j называются соответ ственно начальной и конечной. Путь Sq записывается также в виде последовательности вершин: = (i₀, /_t,…, ij).

Длиной пути s_xj (обозначается 1еп5_/;) называют число / ребер, составляющих путь. Если в графе Г имеется путь s_xj длины /, то вершина j графа I-достижима (или достижима за / шагов) из вершины /. Если ребро или дуга {iyj) (вершина /) принадлежит пути, то говорят, что путь проходит через ребро или через дугу (у) (через вершину /).

На множестве путей графа определена частичная полугрупповая операция конкатенации (присоединения), обозначим ее •. Для путей s_xj и s_uv конкатенация допустима j = u. Если конкатенация допустима, то len(s^ • s_{u v}) = = 1еш^ + 1еп5_м

Теорема 3.2. Пусть М — матрица смежности вершин графа Г и М' = (mjp), тогда число путей длины t из г в у в графе Г равно mfp, i, j е {1…п).

4 (индукция по t). Для t= 1 теорема верна по определению матрицы М.

Докажем теорему для t и любых /, у, если она верна для t — 1 и любых г, у.

По определению М' = М^ММ, тогда по правилу умножения матриц.

По предположению трравно числу путей длины (- 1 в графе Г из вершины г в вершину s. Тогда тр^тр есть число путей длины У в Г из г в у таких, что s предшествует вершинеу. Просуммировав по s, получаем общее число путей длины t в графе Г из вершины / в вершину у, которое в силу (3.1) равно тр. ?

При г =у путь Sq называется циклом (в орграфе — контуром). Петля есть цикл длины 1. Вершина графа, принадлежащая какому-либо циклу, называется циклической, не принадлежащая ни одному циклу — ациклической. Граф называется циклическим (ациклическим), если он содержит (не содержит) циклы.

Путь (цикл) называется простым, если он не проходит дважды ни через одну вершину. Простой путь (цикл) в графе не проходит дважды ни через одно ребро, поэтому принято считать, что в графе длина простого цикла не равна 2 (в орграфе этого ограничения нет).

Путь (цикл), проходящий через все вершины графа, называется полным. Циклы в графе Г называются независимыми, если не пересекаются множества вершин этих циклов.

Подходом к циклу называется путь в графе, все вершины которого, за исключением последней, являются ациклическими.

Неориентированный (ориентированный) граф Г связен (сильно связен), если найдется путь в Г, соединяющий любые его две вершины. Г — связный орграф, если связен неориентированный граф, полученный из Г заменой дуг на ребра.

Замечание. При п > 4 в п-вершинном сильно связном орграфе Г имеется полный цикл длины не более (п² — п) / 2 [13]. Эта оценка совпадает по порядку с точной оценкой. Например, в графе с множеством дуг {(2п, г), (г, п + 1), г = 1,…, п} и {(у, у + 1), у = п + 1, п + 2,…, 2п — 1} и с 2п вершинами длина полного цикла равна п{п +1).

Пусть S (i, j) — множество всех путей из г в у в 2г-вершинном графе Г, г, у е {1,…, п). Величину p_r(i, y) = min lens называют длиной кратчайшего пути

seS (i.j)

из г в у в графе Г (или расстоянием от г до у в графе Г), а всякий путь из г в у длины р_г(г', у) называют кратчайшим путем в Г из г в у. Пусть Y, Z с X. Расстоянием от У до Zb графе Г называют величину р_г(У, Z):

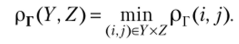
Эксцентриситетом вершины i (обозначается ext/) называется величина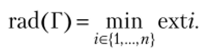

Радиусом связного орграфа (неориентированного графа) Г называется величина.

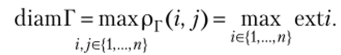
Вершину i называют центром графа, если ext/ = rad (Г). Центров в Г может быть несколько.

Диаметром «-вершинного сильно связного орграфа (связного неориентированного графа) Г называется величина.

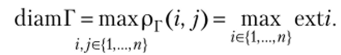
Из равенства сНатГ = t следует, что p_r(i, j) < t для любой пары вершин (i_fj) графа Г и p_r(a, w) = t для некоторой пары вершин (v, w) графа Г.

Теорема 3.3. Диаметр «-вершинного сильно связного орграфа не больше п.

М Из сильной связности графа следует, что для любой пары его вершин (i, j) найдется путь из i в j некоторой длины t. Если t < «, то теорема верна. Если t > п + 1, то данный путь содержит t + 1 вершину, где t + 1 > > п + 2. Следовательно, путь проходит более одного раза через некоторую вершину г, не являющуюся одновременно началом и концом пути. Часть пути, заключенная между первым и вторым прохождением через вершину г, является циклом. Удалим из рассматриваемого пути этот цикл, заменив его вершиной г. В результате получим путь, также идущий из i в j_y но уже более короткой длины.

Будем удалять циклы, пока не получим путь длины не больше п. Следовательно, в графе Г длина кратчайшего пути из i в j не превосходит «для всех i_fj g {1,…, «}. ?

Данная оценка достижима, диаметр полного цикла длины п равен п. Оценка может быть улучшена для частных классов «-вершинных сильно связных графов.