Метод сигнальных графов

Решение уравнений электрического равновесия сложных цепей даже приближенными численными методами, как правило, является весьма трудоемким. Задача анализа цепи становится особенно сложной в случае, когда неизвестные токи и напряжения или комплексные частотные характеристики должны быть найдены в виде аналитических соотношений. При этом полезным может оказаться применение метода сигнальных графов, который позволяет упростить решение уравнений электрического равновесия линейных электрических цепей в аналитическом виде (символьной форме).

Как отмечалось в п. 1.4, сигнальный граф или направленный граф прохождения сигналов представляет собой наглядное графическое изображение системы уравнений, описывающей процессы в электрической цепи. Узлы (вершины) такого графа соответствуют входящим в эту систему неизвестным величинам (токам и напряжениям ветвей, контурным токам, узловым напряжениям) и величинам, характеризующим внешние воздействия на цепь (токам независимых источников тока, ЭДС независимых источников напряжения, контурным ЭДС, узловым токам). Ветви сигнального графа отображают причинно-следственные связи между величинами, соответствующими отдельным узлам. В рамках метода сигнальных графов эти величины называются сигналами. Каждой ветви сигнального графа приписывается определенное направление и присваивается весовой коэффициент, который называется передачей ветви. Узлы сигнального графа обозначают теми же буквами, что и соответствующие узлам величины; направления ветвей показывают стрелками, около которых указывают передачу ветви.

Если ветвь с передачей А направлена от узла х, к узлу х_у- (рис. 4.20, а), то.

Следовательно, при прохождении через ветвь сигнал умножается на передачу ветви. Разрешим уравнение (4.30) относительно Х{.

Сигнальный граф, соответствующий этому уравнению (рис. 4.20, б), отличается от сигнального графа, соответствующего уравнению (4.30), направлением и передачей ветви. Таким образом, вид сигнального графа зависит от того, относительно какой из величин разрешено заданное уравне;

Рис. 4.20. Сигнальные графы, соответствующие выражениям (4.30) и (4.31).

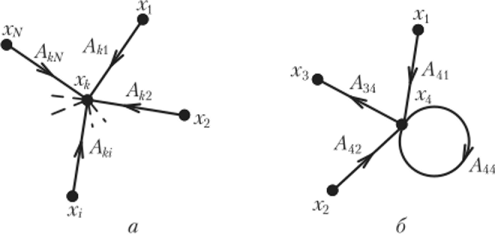
Рис. 4.21. Суммирование сигналов в узле сигнального графа.

ние, т. е. от того, какая из величин рассматривается как причина, а какая — как следствие.

Если в узле х* сходится несколько ветвей (рис. 4.21, а), то значение сигнала в этом узле равно сумме сигналов всех входящих в него ветвей:

где N — число ветвей, направленных к узлу х^_у А^ — передача ветви, направленной от узла х_х к узлу х^.

Ветви, направленные от узла х^ не влияют на его сигнал и при подсчете х* не учитываются. В число ветвей, направленных к исследуемому узлу, могут входить и ветви, начинающиеся в данном узле (рис. 4.21, б). Такие ветви называются петлями. Значение переменной в узле, к которому подключены одна или несколько петель, находится по общему правилу (4.32), например, для рис. 4.21, б,.

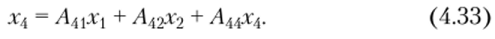
Из выражения (4.33) следует, что при наличии петель, подключенных к какому-либо узлу, переменная, соответствующая этому узлу, входит и в левую, и в правую части уравнения (4.32).

Рассмотрим некоторые понятия, относящиеся к сигнальным графам.

Истоком называется узел сигнального графа, от которого направлены все примыкающие к нему ветви. Узел сигнального графа, к которому направлены все примыкающие к нему ветви, называется стоком. Узлы, которые имеют как входящие, так и исходящие ветви, называются смешанными. Например в графе (см. рис. 4.20, а) узел х_х — исток, узел х_} — сток; в графе (см. рис. 4.21, б) узлы x_h и х₂— истоки, узел х₃ — сток, узел х₄ — смешанный.

Если сигнал, соответствующий некоторому узлу сигнального графа, не выражается через сигналы других узлов, то такой узел является независимым. Если сигнал, соответствующий какому-либо узлу, выражается через сигналы других узлов, то такой узел является зависимым. К независимым узлам относятся истоки, к зависимым — стоки и смешанные узлы. Очевидно, что уравнения вида (4.32) могут быть составлены только для зависимых узлов.

Пример 4.16. Построим систему уравнений, соответствующую сигнальному графу (рис. 4.22). В этом графе узлы x-j — истоки, узел х$ — сток, узлы х_[у х₂, х$, — смешанные. Для зависимых узлов Х —х$ можно составить следующую систему уравнений: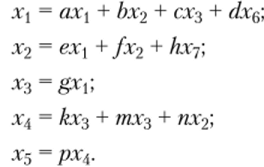

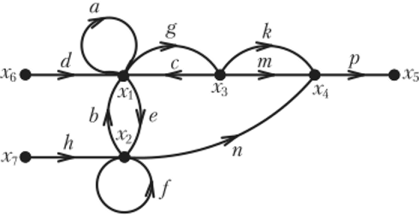
Рис. 4.22. К примеру 4.16.

Путь между узлами Xj и х-_} сигнального графа — это непрерывная последовательность однонаправленных ветвей, связывающая узел Xj с узлом Xj и проходящая через каждый узел графа не более одного раза. Произведение передач ветвей, образующих путь между узлами х, и, называется передачей пути Pji Так, между узлами х₆ и х₅ сигнального графа (см. рис. 4.22) можно указать три пути с передачами = dgkp (ветви d, g, k и р), Р⁽^ = dgmp и Pf$ = denp. Последовательность ветвей d_y с, т, р не образует пути от вершины х$ к вершине так как направление ветви с не совпадает с направлением пути.

Замкнутый путь, который начинается и заканчивается в одном узле, называется контуром. Очевидно, что петля есть частный вид контура, в который входит одна ветвь. Произведение передач всех ветвей, входящих в j-й контур, называется передачей контура L_y На рис. 4.22 можно выделить четыре контура с передачами L = be (ветви b и е)_} L₂ = gc (ветви g и с), 1₃ = а (петля а) и 1₄ = / (петля /). Ветви кит не образуют контура, так как они не представляют собой замкнутой последовательности однонаправленных ветвей. Такие ветви называются параллельными.

Два контура или контур и путь называются соприкасающимися, если они имеют общие узлы. Если два контура или контур и путь не имеют общих узлов, то они являются ^соприкасающимися. На рис. 4.22 контуры с передачами L₂ = gc и =/, L$ = а и L/₄ =/— несоприкасающиеся, а контуры с передачами L_x = be и L₂ = gc, L = be и L₄ = /, L_{ = be и L₃ = <7 — соприкасающиеся. Контур с передачей Z₄ = / не соприкасается с путями и, но соприкасается с путем Как очевидно из примера 4.16, каждому сигнальному графу можно однозначным образом поставить в соответствие систему линейных алгебраических уравнений, составленных относительно сигналов зависимых узлов. Для решения обратной задачи — построения сигнального графа, соответствующего заданной системе уравнений, эта система уравнений должна быть приведена к причинно-следственной форме, т. е. каждое из входящих в систему уравнений должно быть разрешено относительно одной из переменных (различных для каждого из уравнений). Далее определяется общее число узлов графа N, которое равно сумме числа неизвестных переменных и числа ненулевых свободных членов, входящих в систему уравнений. Построение сигнального графа начинается с нанесения точек, соответствующих его узлам. Затем узлы графа в соответствии с системой уравнений, приведенной к причинно-следственной форме, соединяются между собой ветвями так, чтобы сумма сигналов всех ветвей, сходящихся в каждом узле, равнялась бы сигналу этого узла. Для повышения наглядности изображения рекомендуется располагать истоки в левой части чертежа, стоки в правой, а остальные узлы — между ними.

В связи с тем, что одну и ту же систему уравнений можно различными способами привести к причинно-следственной форме, каждой системе уравнений можно поставить в соответствие некоторое множество графов. Различные графы, соответствующие одной и той же исходной системе уравнений, называются равносильными.

Рассмотрим несколько примеров построения графов, соответствующих заданной системе уравнений.

Пример 4.17. Построим сигнальный граф, соответствующий системе уравнений.

Приведем данную систему уравнений к причинно-следственной форме, для чего разрешим первое уравнение относительно Лф второе — относительно д:₂, а третье — относительно х$.

Число независимых переменных в этой системе уравнений равно трем, число ненулевых свободных членов — двум, следовательно, общее число узлов сигнального графа равно пяти. Располагая в левой части чертежа независимые узлы, соответствующие свободным членам Ь_у и й₂>а в правой части узлы, соответствующие неизвестным величинам Х> д:₂, х3, и соединяя их ветвями в соответствии с системой уравнений, преобразованной к причинно-следственной форме, получаем сигнальный граф, изображенный на рис. 4.23, а.

Исходная система уравнений может быть приведена к причинно-следственной форме и другим способом. Прибавляя к правой и левой частям первого уравнения Х, второго дг₂, третьего х$ и выполняя очевидные преобразования, находим.

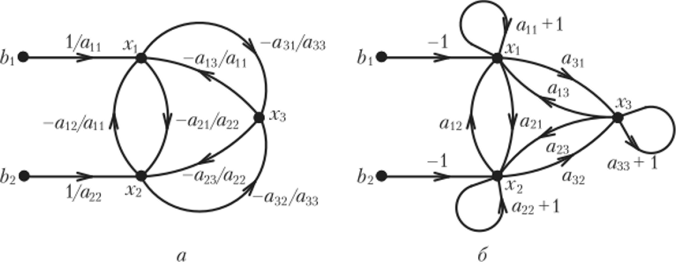
Рис. 423. К примеру 4.17.

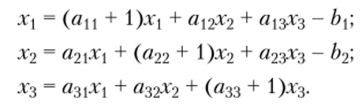
Этой системе уравнений соответствует сигнальный граф, изображенный на рис. 4.23, б.

Графы (см. рис. 4.23, а, б) имеют различную структуру и передачи ветвей, однако они соответствуют одной и той же исходной системе уравнений и поэтому являются равносильными. Очевидно, что если первое уравнение, входящее в исходную систему, разрешить не относительнох, а относительно^ или дгз, то получатся другие варианты представления исходной системы уравнений в причинно-следственной форме, каждому из которых можно поставить в соответствие сигнальные графы, равносильные графам, изображенным на рис. 4.23.

Пример 4.18. Составим сигнальный граф, соответствующий узловым уравнениям цепи, схема которой приведена на рис. 4.2, а.

Узловые уравнения данной цепи были составлены при рассмотрении примера 4.5. Разрешая первое из этих уравнений относительно, а второе — относительно U20, получаем.

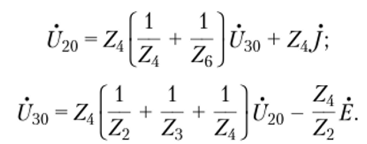
Этой системе уравнений соответствует сигнальный граф, приведенный на рис. 4.24.

Рис. 424. К примеру 4.18.

Пример 4.19. Используя метод контурных токов, составим систему уравнений для определения тока цепи, схема которой приведена на рис. 4.2, а. Построим сигнальный граф, соответствующий этой системе уравнений.

Контурные уравнения исследуемой цепи были сформированы при рассмотрении примера 4.4. Дополняя эти уравнения соотношением, связывающим ток /₆ с контурными токами 7ц и /₂2, получаем.

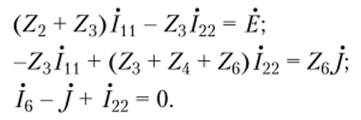
Разрешим каждое из этих уравнений относительно одной из неизвестных величин:

Этой системе уравнений соответствует сигнальный граф, изображенный на рис. 4.25.

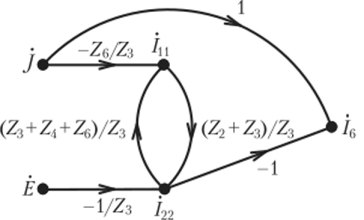
Рис. 4.25. К примеру 4.19.