Общая структура балансового уравнения

Балансовые уравнения всегда имеют одинаковую структуру независимо от того, что является объектом составления баланса — масса, энергия, энтропия или деньги.

Первый шаг составления баланса заключается в выборе объекта для анализа и пространства баланса. Например, бухгалтер при составлении баланса выбирает деньги в качестве объекта анализа, а в качестве пространства баланса выступает счет. При составлении баланса бухгалтер исследует движение денег на счете за некоторый промежуток времени. Перевод денег на счет увеличивает количество денег на счете, а платежи уменьшают их.

Переходя к термодинамике, отметим, что пространством баланса является термодинамическая система. Если некоторое количество X объекта исследования передается через границы системы из окружающей среды, то количество X в системе возрастает. Если X выводится в окружающую среду из системы, его количество в системе убывает. Кроме того, возможно существование источников и стоков X в системе, за счет которых содержание X в системе может изменяться.

При составлении баланса для части системы, например массы газа С0₂, источником будет реакция образования этого газа (например, горение угля), а стоком — реакция, в которой С0₂ разлагается (например, реакция фотосинтеза). Для энергии не существует источников и стоков.

Общую структуру балансового уравнения для объекта X в системе в дифференциальной форме можно представить как.

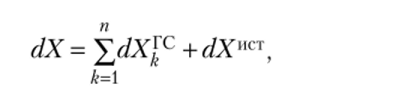
где dX^llCT — источниковый член (рис. 3.1); dXj_t^c — вклад &-го канала, по которому происходит обмен X со средой через границы системы (ГС). Это слагаемое положительно, если объект транспортируется в систему, и отрицательно, если он выводится из системы.

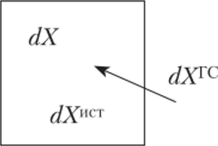
Рис. 3.1. К понятию структуры балансового уравнения.

Если рассматривается изменение системы при переходе из состояния 1 в состояние 2, то имеет место интегральное соотношение.

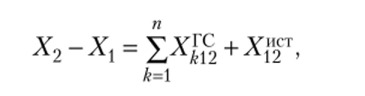
которое получено в результате интегрирования дифференциального соотношения на участке 1—2.

Если рассматривается процесс на промежутке времени dx, тогда можно записать уравнение баланса в виде.

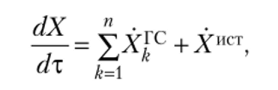
где dX / dx — скорость изменения величины X в системе; Щ^с — приток или отток X через границы системы в единицу времени по k-му каналу (поток величины X); Х^ист — скорость производства или уничтожения X в системе.

Формула Гаусса — Остроградского. В [1] показано, что если в некоторой области (V) определены функции Р (х, г/, z), Q (х, г/, 2), R (х, у, 2), непрерывные со своими производными ЭР/Эх, dQ/dy, dR/dz во всей области (V) и на ее границе (S), то справедливо соотношение.

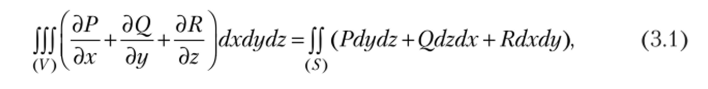
которое связывает интеграл по объему области (V) с интегралом по поверхности этой области (S). Данное соотношение называется формулой Гаусса — Остроградского. Другая форма записи соотношения (3.1) имеет вид.

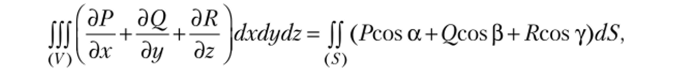
где а, р, у — углы, образуемые внешней нормалью к поверхности (5) с координатными осями.

Если в точке М задано векторное поле Л (М), тогда поверхностный интеграл

называется потоком вектора А через поверхность (S) в указанную сторону [1].

Если в формуле Гаусса — Остроградского положить Р = А_х, Q = А, R = A_v то поток вектора А через поверхность (5) наружу можно преобразовать в тройной интеграч:

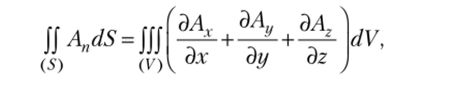
Э А ЭД^ ЭЛ — —.

где -^ + —^- + —^ = сН^гЛ — дивергенция вектора Л.

Эх ay dz

Теперь, с учетом сказанного, формулу Гаусса — Остроградского можно записать так: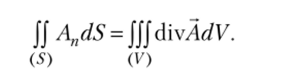

На практике чаще применяется другое определение дивергенции, которое не зависит от выбора системы координат:

Под дивергенцией векторного поля обычно понимают количество векторных линий, начинающихся в бесконечно малом объеме М, отнесенное к единице этого объема [2].

Формула Гаусса — Остроградского применяется при анализе потоков энергии и вещества. Эту формулу можно рассматривать как балансовое уравнение для случая непрерывного изменяющихся потоков. Физический смысл ее можно выразить следующим образом: поток векторного поля через замкнутую поверхность равен объемному интегралу дивергенции по этой поверхности. Иными словами, из данной формулы следует, что суммарный поток из некоторой области равен суммарному потоку в эту область плюс сумма источников в самой области.

В качестве примера приведем движение несжимаемой жидкости с источником, описываемое соотношением.

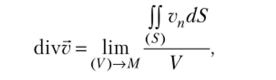
в котором JJ v_ndS — поток вектора скорости; divn — плотность источников.

(S)

При этом предполагается, что источники распределены непрерывно по рассматриваемой области. Поток вектора скорости характеризует производительность источников внутри замкнутой поверхности (S), это количество жидкости, вытекающей через поверхность (5) в единицу времени. Аналогичное соотношение можно получить для вектора потока тепла [1].