Двухволновое приближение в совершенном кристалле

Точки Лоренца и Лауэ.

Система уравнений (1.69) в общем случае должна состоять из бесконечного числа уравнений, однако даже беглый анализ системы показывает, что величины Dm резко уменьшаются с ростом разности К2 — к2. Действительно, правая часть системы не может сильно изменяться при переходе от одного уравнения этой системы к другому, т. е. Dm велико, если разность К2 — к2 мала. Это означает, что значениями Dm для всех членов с большой разностью К2 — к2 можно пренебречь ввиду их малости. Тогда число уравнений в системе (1.69) можно ограничить.

Наибольший практический интерес представляет случай, когда ориентация кристалла близка к одному из брэгговских положений, например к положению с волновым вектором (вектор отражения) К_г, т. е. когда только два узла обратной решетки с индексами 0 и 1 (индексы Миллера которых соответственно (000) и (Ш)) лежат вблизи сферы Эвальда. Такой случай, названный двухволновым приближением [6, 7], показан на рис. 1.18, где точка L соответствует случаю, когда коэффициент преломления равен единице (т.е. рассеяние происходит в вакууме), и называется точкой Лоренца. Точка М соответствует центру распространения волн с учетом преломления, но для кинематического случая, когда взаимодействием волн можно пренебречь. На рис. 1.18 обозначения Т₀ и Т_н — следы от пересечения сфер Эвальда радиусами Ко и К_н, проведенных из узлов обратной решетки 0 и Я. Точка их пересечения — точка М называется точкой Лауэ. Так как для рентгеновского диапазона длина волны составляет порядка 1 А, поверхности Т₀ и Т_н вблизи брэгговского отражения в интервале десятка угловых секунд являются практически плоскостями.

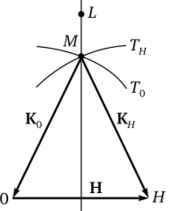
Рис. 1.18. Геометрия расположения волновых векторов для случая двух сильных волн:

Н — вектор магнитной индукции В двухволновом случае в решении волнового уравнения (1.69) остается только два члена:

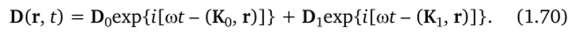
Тогда система уравнений (1.69) будет состоять только из двух уравнений:

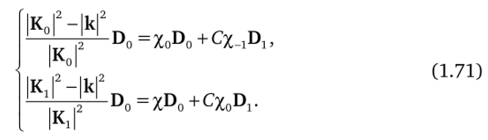
Дисперсионное уравнение. После несложных преобразований система (1.71) может быть записана в матричной форме:

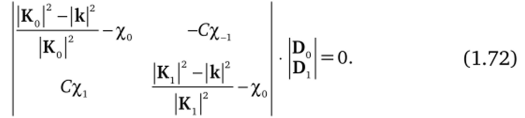
Система линейных уравнений (1.72) будет иметь нетривиальные решения, если детерминант системы тождественно равен нулю, т. е. когда выполняется равенство.

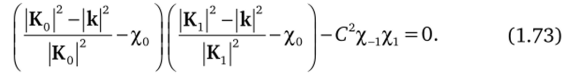
Здесь поляризационный множитель С = 1 для компонент волнового поля, поляризованных перпендикулярно к плоскости рассеяния (ст-поляризация), и С = cos 20 для компонент, поляризованных в этой плоскости (л-поляризация), где.

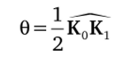
есть брэгговский угол.

Уравнение (1.73) описывает двухлистную поверхность вращения типа гиперболического цилиндра с осью вращения, совпадающей с вектором обратной решетки Н, называемым вектором дифракции или вектором отражения, и асимптотами Т₀, Т_И, и носит название дисперсионного уравнения. Расщепление дисперсионной поверхности на два листа обусловлено связью проходящей и дифрагированной волн в динамическом случае внутри треугольника рассеяния. Это общее явление в случае связанных колебаний и волн. Сечение дисперсионной поверхности плоскостью рассеяния для двухволнового случая изображено на рис. 1.19.

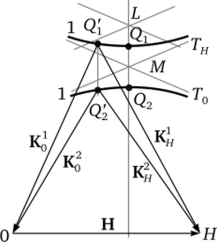
Рис. 1.19. Сечение дисперсионной поверхности плоскостью рассеяния для двухволнового случая:

1,2 — кривые, соответствующие двум листам дисперсионной поверхности; Q₁₍ Q₂ — связанные точки возбуждения в точном брэгговском положении, соответствующие двум типам блоховских волн; Т₀, Т_н — следы сфер распространения радиусом 1/Х Дисперсионные уравнения позволяют в каждом конкретном случае определить амплитуды всех волн, участвующих в рассеянии и, следовательно, определить интенсивности всех дифракционных пиков.

Маятниковый эффект. Не вдаваясь в детали вывода, можно получить выражения, связывающие коэффициенты прохождения Г (0) и отражения Я (0) волн с величиной дифракционного угла, и таким образом построить профили дифракционных линий, однако в общем случае выражения эти достаточно громоздки. Для симметричного лауэвского случая дифракции рентгеновских лучей на плоскопараллельной пластинке при отсутствии поглощения эти соотношения имеют вид.

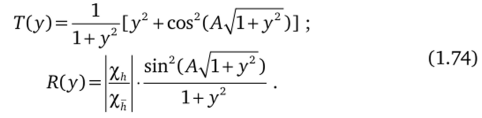
Здесь у — текущая координата, определяемая углом дифракции;

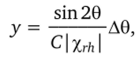
где 0 — брэгговский угол; С — коэффициент поляризации; %rh — действительная часть Фурье-компонеты поляризуемости кристалла для выбранной системы отражающих плоскостей; А — относительная толщина кристалла в экстинкционных длинах;

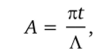
где t — толщина кристалла, мкм; Л — экстинкционная длина, мкм;

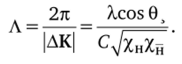
Из соотношений (1.74) с очевидностью следует, что как проходящая, так и отраженная волны зависят не только от величины угла А0, но и от толщины кристалла t. На рис. 1.20 показан характер изменений коэф;

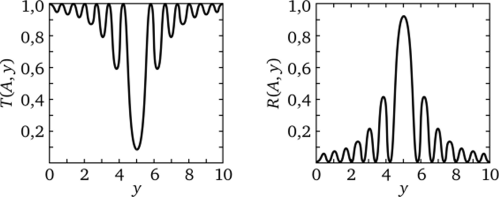
Рис. 1.20. Характер изменений коэффициентов прохождения Т (А, у) и отражения R{A, у) в окрестности брэгговского максимума.

фициентов прохождения Т (А, у) и отражения R (A, y) вблизи максимума брэгговского отражения для случая плоскопараллельной кристаллической пластинки. Эти зависимости имеют осциллирующий характер и быстро убывают с увеличением отклонения от точного брэгговского положения за счет множителя (1 + у²)^-1.

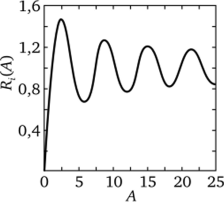
Рис. 1.21. Осциллирующий характер зависимости интегрального коэффициента отражения /?,(Д) от толщины кристалла в экстинкционных длинах А (А = ntIA).

Чтобы проследить изменение коэффициентов Т (А, у) и R (A, y) с изменением толщины кристалла, необходимо проинтегрировать выражения (1.74) по параметру у, определяемому величиной отклонения от брэгговского положения. Зависимость интегрального коэффициента отражения от параметра А показана на рис. 1.21, из которого следует, что интенсивность дифрагированного пучка осциллирует с увеличением толщины кристалла. Аналогичным образом ведет себя и проходящая волна. Этот эффект впервые был обнаружен (теоретически) П. Эвальдом (1916) и получил название маятникого эффекта. Такое поведение интенсивности дифрагированной и отраженной волн связано со взаимной перекачкой энергии между этими волнами и совершенно аналогично перекачке энергии между двумя связанными маятниками (отсюда и название эффекта).