Современные модели экономического роста

В настоящее время, кроме классических теорий экономического роста, чаще всего встречаются неоклассические и неокейнсианские модели.

В неоклассических моделях принимаются следующие исходные условия: 1) стоимость любого блага — результат всех факторов производства, каждый из которых вносит в ценность свою долю; 2) экономике капитализма свойственны все условия ее саморегулирования и свободной конкуренции. Основной объект анализа неоклассиков — труд и капитал как факторы экономического роста. Метод их исследования включает: 1) анализ влияния количественных изменений в факторах производства (в объемах капитала и труда) на экономический рост; 2) анализ влияния качественных изменений в факторах (в качестве капитала и труда — НТП, изменения в организации производства, в качестве рабочей силы) на экономический рост. Цель исследования — поиск наиболее эффективной структуры капвложений и оптимального уровня экономического роста. Инструмент исследования — производственная функция.

При этом неоклассики используют известную нам (см. гл. 13) производственную функцию (модель) Кобба — Дугласа, которую они интерпретируют в соответствии с теорией убывающей предельной полезности капитала и труда при неизменной их совместной производительности. Функция Кобба — Дугласа, напомним, раскрывает зависимость совокупного продукта (Q) от двух факторов — труда (L) и капитала (К): Q = F (LK).

Позднее Р. Солоу, Э. Денисон, Д. Мид и другие неоклассики модифицировали эту функцию путем ввода в нее других факторов роста: фактора времени, возраста основного капитала, масштаба производства, квалификации работников и т. п. В связи с тем что уровень технологий со временем постепенно совершенствуется, в уравнение Кобба — Дугласа вводится фактор времени, и производственная функция принимает следующий вид:

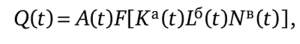
где Q (t) — объем производства за период времени t; А (0 — коэффициент, отражающий ускорение НТП за период времени t; K (t), L (t), N (t) — затраты соответственно капитала (К), труда (L), ресурсов природы (N) за период времени t; а, б, в — коэффициенты эластичности объема производства соответственно по капиталу (К), труду (L), природным ресурсам (N). Эти коэффициенты отражают объем производства, который вызывается приростом на 1% соответствующих факторов экономического роста.

Таблица 24.2

Вклад факторов экономического роста в прирост ВВП США (данные Э. Денисона, в среднем за 1929—1982 гг., %)

Производственная функция позволяет определить, за счет каких факторов достигается данный экономический рост и степень влияния на этот рост каждого из факторов. Так, Э. Денисон, основываясь на анализе эмпирических материалов за 1929—1982 гг., предложил классификацию источников экономического роста, содержащую 23 фактора. По его данным, с 1929 по 1982 г. ВВП США в среднем ежегодно увеличивался за счет трудозатрат на 32% и за счет роста производительности труда — на 68%. А рост производительности труда достигался за счет НТП (на 28%), затрат капитала (19%), образования и профессиональной подготовки кадров (14%), экономии, обусловленной масштабами производства (9%), улучшения распределения ресурсов (8%), законодательно-институциональных и других факторов (-9%). Последняя группа факторов сдерживает экономический рост, что вызывается отвлечением средств на улучшение условий производства, среды обитания и т. п. В перспективе эти затраты обычно способствуют росту производительности труда и экономическому росту.

Неокейнсианские модели экономического роста рассмотрим на примерах моделей американского экономиста Евсея Домара (1914— 1997) и английского экономиста Роя Харрода (1900—1978). Отличие их моделей от модели Дж. Кейнса заключаются в следующем:

• 1) Кейнс предполагал, что запас капитала остается постоянным, а Домар и Харрод учитывают то, что инвестиции имеют двоякий характер: а) создают доход и б) расширяют капитальный запас, увеличивают ресурсы предпринимателя. Чистые инвестиции уже по определению представляют собой скорость изменения капитального запаса в единицу времени;
• 2) Кейнс формулировал задачу устранения чрезмерной безработицы, а Домар и Харрод подняли более сложный и общий вопрос: найти пути обеспечения устойчивых темпов роста капиталистической экономики;
• 3) в моделях экономического роста Домара и Харрода сделана попытка обобщить процессы, рассматриваемые в рамках кейнсианской модели, распространив их с краткосрочного на долгосрочный период;
• 4) Домар и Харрод вводят в свой анализ показатели технического прогресса, концентрируют внимание на количественном анализе воспроизводства и на функциональных зависимостях.

Модели Харрода и Домара основаны на следующих предпосылках: 1) накопление и экономический рост являются взаимообусловленными процессами; 2) рост НД определяется только нормой накопления капитала, а все другие факторы (рост занятости, степень использования оборудования, улучшения в организации производства, которые отражаются на росте капиталоотдачи) исключаются. Поэтому спрос на капитал при данной капиталоемкости определяется только темпом роста НД; 3) капиталоемкость не зависит от прибыли и заработной платы, а определяется только техническими условиями производства. Связь между долей инвестиций в НД и капиталоемкостью строится на основе равенства сбережений и инвестиций. Причем сбережения характеризуют предложение фондов для инвестирования, а величина инвестиций определяется спросом на эти фонды.

Однако модели Р. Харрода и Е. Домара имеют следующие различия.

Назначение модели Харрода — поиск условий, обеспечивающих равновесный экономический рост. Полагая, что предложение сбережений является устойчивой функцией потребления, а спрос на инвестиции зависит от темпов роста НД и величины капиталоемкости, Харрод, в частности, предложил формулу равенства сбережений и инвестиций:

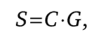
где S — доля сбережений в НД; С — капиталоемкость; G — темп роста НД.

Из этой формулы выводится уравнение динамического равновесия:

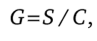
где G — темп роста НД; S — сбережения, которые в долгосрочном периоде являются постоянными вследствие устойчивости функции потребления; С — требуемая капиталоемкость.

Другими словами, уравнение (условие) динамического равновесия заключается в следующем: если величина капиталоемкости постоянна — требуемая капиталоемкость С, а доля сбережений S в долгосрочном периоде имеет тенденцию оставаться неизменной, то темп роста НД (G) должен быть постоянным, он определяется по указанной формуле G = S/C.

В основе модели Домара лежит равенство денежного дохода (спроса) производственным мощностям (предложению), а не равенство сбережений и инвестиций (как это делает Харрод).

Назначение модели Домара — найти величину инвестиций, темп их роста и этим сделать прирост дохода равным приросту производственных мощностей. Для этого Домар предложил следующее уравнение:

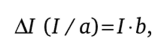
где ДI — прирост объема инвестиций I; а — мультипликатор инвестиций; b — потенциальная средняя производительность инвестиций;

т.е. левая сторона уравнения А/ (//а) — прирост объема инвестиций I к мультипликатору 1/а — составляет прирост дохода в денежном выражении, а его правая сторона I • b — произведение инвестиций I на потенциальную среднюю производительность инвестиций b дает прирост производственных мощностей.

Из уравнения Л/ (I/a) = I • Ъ Домар выводит второе уравнение:

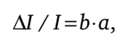
которое характеризует полную загрузку производственных мощностей и темп прироста инвестиций (AI/I), который равен произведению доли сбережений а на потенциальную среднюю производительность инвестиций Ь.

И Домар, и Харрод пришли к выводу, что условием динамического равновесия при постоянной норме накопления и постоянной капиталоемкости является устойчивый темп роста НД. Этот темп роста Харрод назвал гарантированным. Отклонение от гарантированного темпа роста порождает, по Харроду, кумулятивные причины, побуждающие фактический темп роста отклоняться от линии равновесия. На трудности поддержания условий динамического равновесия экономики капитализма указывал и Домар.