Вопросы и задания для повторения

• 1. Что называется повторными независимыми испытаниями Бернулли? Привести пример таких испытаний.
• 2. Сформулировать и доказать теорему Бернулли.
• 3. В каких пределах заключено наивероятнейшее число успехов в серии из п независимых испытаний Бернулли с вероятностью р в одном испытании?
• 4. Какие испытания называются полиномиальными?
• 5. Сформулировать и доказать теорему о полиномиальных испытаниях.
• 6. Сформулировать и доказать закон редких событий.
• 7. Сформулировать локальную и интегральную теоремы Муавра—Лапласа.
• 8. Привести формулу функции Лапласа. Указать ее свойства и нарисовать график функции.
• 9. Чему равна вероятность того, что относительная частота появления успеха
• — в п независимых испытаниях Бернулли отклонится от вероятности успеха

п

не более, чем на е > 0? Обосновать.

Примеры решения задач

Задача 3.1. В роддоме за сутки родилось 10 детей. Найти вероятность того, что ровно пять из них — мальчики, если по статистике вероятность рождения мальчика равна 0,51.

Решение. Считаем рождение мальчика «успехом» в серии из 10 рождений, в каждом из которых «успех» появляется с вероятностью р = = 0,51. Вероятность того, что «успех» в 10 испытаниях появится ровно пять раз, равна Р₁₀(5) = С^₀ 0,51⁵ 0,49⁵ «0,2456.

Задача 3.2. В эксперименте, состоящем из п независимых испытаний, вероятность двух успехов в 10 раз больше вероятности одного успеха. Найти число испытаний, при котором вероятность успеха в одном испытании будет наибольшей.

Решение. Составим уравнение с двумя неизвестными: п — числом испытаний и р — вероятностью успеха:

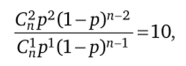
где п > 2.

После преобразований имеем -—- ^ =10, откуда р=—.

2 1-р 19 + гс Поскольку с ростом п функция вероятности убывает, возьмем п = 2. Тогда р_тах =|р Ответ: п = 2.

Задача 3.3. При соблюдении технологического режима среднее число бракованных деталей составляет 2 ед. на 100 ед. продукции. При выборочном контроле проверена партия из 20 деталей, среди которых попалась бракованная деталь. Есть ли основания полагать, что имеются нарушения технологического режима?

Решение. Среди проверенных деталей могло оказаться любое количество бракованных деталей в пределах 0 < т < 20 с разной степенью вероятности. Разумно сравнить вероятность отсутствия бракованных деталей с вероятностью их наличия:

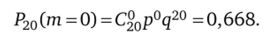
Тогда Р₂₀(т > 1) = 1 — 0,668 = 0,332.

Вывод. В партии из 20 проверенных деталей вероятнее, что брак должен отсутствовать. Есть основания полагать, что технологический режим нарушен.

Задача 3.4. Общественное транспортное средство с 12 пассажирами делало на маршруте остановки для высадки пассажиров. Найти вероятность того, что по два пассажира выйдут на трех остановках и по три пассажира — на двух остановках, если: а) это маршрутное такси, делающее остановки по требованию; б) это рейсовый автобус, останавливающийся на каждой из 10 остановок общественного транспорта.

Решение, а) Движение такси с остановками можно рассматривать как полиномиальные испытания с пятью разными исходами, поскольку водитель заранее информируется пассажирами о числе остановок. Вероятности исходов равны 0,2: каждый из пассажиров с вероятностью 0,2 может выйти на любой из пяти остановок. Пусть из 12 пассажиров двое вышли на первой остановке. Число таких случаев равно С^₂. Два других пассажира вышли на следующей остановке. Число случаев С^₀. Рассматривая следующие остановки, получим соответствующую вероятность равной.

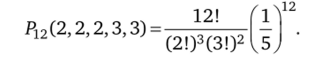
Учтем, что на первой остановке могли выйти три пассажира, на второй — также три, т. е. рассмотрим перестановки чисел 2 и 3. Число.

таких перестановок равно С? =—— = 10.

_ ^{г 5} 3191.

Окончательно имеем '.

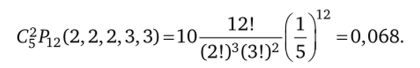
б) Вероятность выхода пассажира на одной из 10 остановок общественного транспорта равна 0,1. Кроме того, надо выбрать пять остановок из 10, на которых выйдут пассажиры. В результате получим.

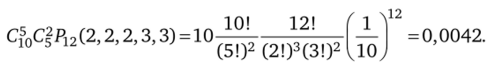
Задача 3.5. В п независимых испытаниях появилось т успехов. Каково наиболее вероятное значение одного успеха?

Решение. Вероятность того, что успех в п испытаниях появится ровно т раз, выражается формулой Р_п (т) = С™р^т (1 — р)^п~^т.

Исследуем вероятность P_n(m) как функцию от р на максимум, для чего возьмем производную и приравняем ее к нулю:

_ m _.

Отсюда следует, что р = —.В этой точке достигается максимум, так п

как только последняя скобка, содержащая линейную по р убывающую функцию, обращается в нуль: т — пр = 0. Ответ: р =—.

п

Задача 3.6. С конвейера сходят готовые детали с вероятностью брака 0,005. Какова вероятность обнаружить не менее трех бракованных деталей среди 1000 проверенных?

Решение. Обнаружение брака посчитаем успехом. Вероятность того, что успех в 1000 испытаниях появится не менее трех раз, может быть вычислена с использованием формулы Бернулли как разность между единицей и суммарной вероятностью обнаружить 0, 1 или 2 бракованные детали:

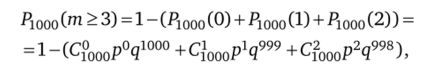
где р = 0,005, q = 1 — р = 0,995. Получим Р₁₀оо (^т — 3) = 0,87 598.

Среди готовых деталей брак встречается редко. Поскольку р = 0,005 < < 0,1 и пр = 5 < 10, можем воспользоваться приближением формулы Бернулли — формулой Пуассона сХ-пр-5:

Результаты отличаются в четвертом знаке после запятой. Расчет по формуле Пуассона — более простой.

Задача 3.7. Производится 200 подбрасываний симметричной монеты. Какова вероятность того, что число выпадений орла будет отличаться от 100 не более чем на пять.

Решение. Пусть т — число выпадений орла при 200 подбрасываниях симметричной монеты, p-q-—, пр = 100. Тогда в соответствии с преобразованием ^.

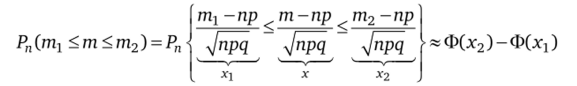
получим.

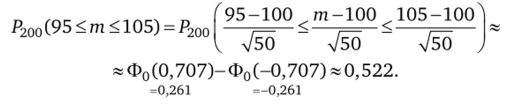
Задача 3.8. Сколько подбрасываний симметричной монеты следует сделать, чтобы с вероятностью 0,997 можно было утверждать, что число выпадений орла не меньше 100?

Решение. Пусть т — число выпадений орла при п подбрасываниях симметричной монеты. Величину п следует искать из условия Р (т > > 100) = 0,997. Воспользуемся формулой Муавра — Лапласа:

Воспользуемся таблицей Лапласа:

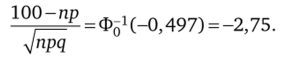
Считаем p = q = Для Vn = x > 0 получим квадратное уравнение x²

— 2,75x- 200 = 0. Находим n, используя положительный корень уравнения:

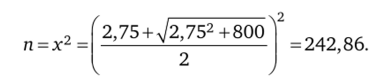
Таким образом, можно утверждать, что при 243 подбрасываниях монеты орел выпадет не менее 100 раз с вероятностью 0,997.