Аксиоматическое введение множества R

Определение 5.1. Множеством действительных чисел называется непрерывное, линейно упорядоченное поле R. Это означает, что, вопервых, на множестве R заданы следующие отношения и операции:

I. Отношение равенства (см. Глава 3, п.п. 3 и 4).

II. Бинарная операция +: R х R —>й и, а + Ь = с есть алгебраическая запись операции +.

III. Бинарная операция ®: R х R —"й и а-Ь = с есть алгебраическая запись операции ®.

IV. Отношение порядка р с й х й я а <�Ь есть алгебраическая запись того, что (а, б) ер (см. Глава 3, п.п. 4 и 5).

Во-вторых, при этом выполнены следующие аксиомы:

• 1.1. аа. 1.2. а = b => b — а .
• 1.3. я = б&б = с => я = с. 1.3'. а = b => (ср (я) => ф (б)).
• 11.1. а + b = b + а. II.2. а + (Ь + с) = (а + Ь) + с.
• 11.3. 30 ей: Уя ей я + 0 = я.
• 11.4. У я ей 3р ей: а + р = 0.

III. 1. я • б = б • я. III.2. а • (b ? с) = (а? b)? с.

Ш. З. 31 ей: Убей ЪЛ=Ь .

111.4. Уя е й{0} 3q е й: a q = .

IV. 1. а < b&b я < с. IV.2. (0, 0) g с, т. е. 0<0 ложно.

IV.3. 0<1. V.I. (я + б) —с = а • с + b? с.

VI.1.У сей я я + с <�б + с.

VI. 2. (я > 0) &(б > 0) => я • б > 0.

VII. Всякое разбиение множества й на верхний В и нижний А классы:

Лий=й, А*0 * В и У (я, б) еЛхй я < б, есть дедекиндово сечение, т. е. либо 3 с е А: Уу е А{с}: у<�с и Уре. В 3beB: b

либо.

3d е В :Ух е В {d} d е А: у<�а.

Замечание 5.5. В Аксиомах 1.2 и 1.3 равенства я = б, Ь = с, а = с означают, что один и тот же элемент обозначен разными символами или даже получен разными способами, например, |я| = -%/я • я (см. также [53, с. 12]). В Аксиоме 1.3' ср (б) — некоторое выражение, не содержащее я (см. с. 12 и далее). Аксиома 1.3' обеспечивает замену равного равным. Из этой аксиомы следуют, в частности, Аксиомы 1.3 и 1.2 (см. также [53, с. 12]).

Замечание 5.6. Аксиомы 1.1−1.3' и доказываемую ниже Теорему 5.4 традиционно и по умолчанию опускают (см. [53, с. 12], ер. [30, с. 40, 41]).

Замечание 5.7. В Аксиоме IV.3 условием 0 < 1 выбрана за положительную одна из двух возможных ориентаций в R. 0 < 1 или 1 < 0.

Замечание 5.8. Использование нестрогого неравенства q < х оправдано лишь в тех выражениях, где, по крайней мере, одна из букв q их сеть символ переменной (см. Глава 1, Соглашение С), иначе, например, вместо 2 < 3 мы пишем 2 < 3.

Весь изучаемый в высшей математике анализ — математический анализ функций — является теорией, выводимой из Аксиом IVII. Отметим здесь лишь некоторые факты, при этом равенство = и импликацию =>, справедливые в силу условия S, мы будем обозначать символами =(S)= и, соответственно.

Теорема 5.0. V (x, jy) e Rx R либо х < у, либо X — у, либо X > у.

• Пусть, например, 3(a, b) e R х R: a>&b>a. Тогда по Аксиоме IV. 1 а > а и по Аксиоме VI. 1 получим 0 > 0, это противоречит Аксиоме VI.2. Если же допустить существование в R {a, b}: а > b и а = Ь, то по Аксиоме 1.3' получим а > а и далее 0 > 0 .?

Теорема5.1. Если 3{0,0}c/f: V{fl, i}cl? а + 0 = а и b + 0=b, то 0 = 0.

• Из условия теоремы при а = 0 и b = 0 получим 0 + 0 = 0 и 0 + 0 = 0. Из этих равенств и Аксиом II. 1 и 1.3 следует, что 0 = 0. ?

Аналогично доказывается единственность в R единицы, то есть Теорема 5.2. al = a& b =b=>l=l.

Определение 5.2. Множеством натуральных чисел назовем множество N с R, определяемое индуктивно двумя условиями (ср. п. 3.6):

• 1) eN.
• 2) Если п еА, то п + 1 е /V.

Теорема 5.3.Если, а + р-0 и a + q-О, то p = q.

• Допустим противное, т. с. что —*(p = q). Если, например, р> q, тогда из а + р> а + q следует 0 > 0. Это противоречит Аксиоме IV.3.B.

Единственное число p-q—a называют числом, противоположным числу а.

Определение 5.3. Число, а назовем положительным и число (-а) назовем отрицательным, если а > 0.

Определение 5.4. Разностью чисел, а и b назовем число с = а + (- b)=a — Ь.

Теорема 5.4. Если, а = Ь, то Ус ей а + с-b + с.

• Допустимл(а + с = b + с), например, а + с > b + с. Из этого неравенства, по Аксиоме VI. 1, получим а > Ь, что вместе с условием Теоремы противоречит заключению Теоремы 5.0.И Следствие 5.1.я = 6а-6 = 0-а = -Ь.

Теорема 5.5. Если, а — b и p-q, то a + pb + q.

• (а-Ъ, р = </) = (Теор. 5.4)=>(a + p = b + p, b + pb + q) = (1.3) => (а + р = b + q) .?

Теорема 5.6. -(-а) = а.

• ((-а) + (- (-а)) = (II. 4.) = 0) = (Тсор. 5.4) => а + (-а) + (- (-а)) =.

= 0+ 0 — (-а) = а =>-(-а) = а.

Теорема 5.7. — (а + b) = -а — b.

• [" /?=- (я + 6) J = (Следствие 5.1) => (-р = -(-(а + Ь))).

= (Теор. 5.6) =>(-/? = а+Ь)= (Теор. 5.4) => — а — b = р. Теперь имеем ((р = -(а + Ь)) &{р = -а — Ь)) => (-(а + Ь) = -а — Ь) .?

Аналогично доказываются следующие три утверждения:

Теорема 5.8. (-1 )-а—а.

Следствие 5.2. (— 1) — (— 1) = 1.

Следствие 5.3. (-*) • у — ~(ху).

Теорема 5.9. (а = Ь)=> (ас = Ьс) =(с * 0)=> (а = Ь).

• • (а = b)=> (а — b = 0), (ас — Ьс = с (а — Ь) = с ? 0 = 0) =>(ас = Ьс),
• (ас = Ьс) -(с Ф 0)=>(а-с-с' = Ь-с-с')=> (а ? 1 = b ? 1) => (а = b) М

Следствие 5.4. Если а? b = 0, то либо а = 0, либо 6 = 0, либо а = b = 0.

Теорема 5.10. Если, а? w = 1 и a-v = 1, то w = v.

• {aw = av) => (a{w — v) = 0). Так как а Ф 0, ибо равенство a = 0 в силу l = a-w = 0 противоречит Аксиоме IV.3, то в силу Следствия 5.4 (w — v = 0) = (Следствие 5.1) => w — v .?

Единственное в Теореме 5.10 число w-v=a^A называют обратным числом для числа а.

Определение 5.5. Частным чисел, а и b называют число

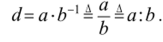
Теорема 5.11. Если, а > 0, то — а < 0.

• (а > о)=> (-а + а > 0 — а)^> 0 > -а.Ш (Ср. [30, с. 38]).

Теорема 5.12. a>-i>0.

• (а > b) = (VI. 1) => (a + {-b)>b + {-b))=>{a-b>0).U

Следствие 5.5. Если, а > Ь и с > 0, то aobc.

• • (а >Ь)= (Теор. 5.12) => (а — b > 0). Поэтому имеем далее (а-Ь>0, о0) = (VI.2) => ((a -b)-c > 0) = (V.1) => (ас — Ьс > 0) =
• (Теорема 5.9) => {ас > Ьс) М

Теорема 5.13. Если, а > Ъ и с > d, то а + с > b + d и a —d> b —с.

• (а > Ь, с > d) = (VI. 1) => (а + с > b + с, b + с > b + d)

= (IV. 1) => (а + ob + d). Неравенство a-d>b-c доказывается аналогично, так как по Теореме 5.12 из с > d следует -d > -с М

Упражнения Доказать следующие свойства действительных чисел:

• 5.14. Если а > b + с, то а — с > b .
• 5.15. Если а Ф 0, то (я) = а .
• 5.16. (- аb) = a? b.
• 5.17. Если а * 0, то (-д)^-1 =-(йг^ч).
• 5.18. Если а > 0, то а~' > 0.
• 5.19. Если а > 1, то 0 < я" ¹ < 1.
• 5.20. Если а > b и с < 0, то ас < Ьс.
• 5.21. При а > b и с > d ас> bd в следующих трех случаях:
• 1) если а > 0 и d > 0,
• 2) если с > 0 и b > 0,
• 3) если b > 0 и d >0.

Утверждение 5.22. /я > 0 З{с, 1)}сй: 0.

Д.

• • Пусть с = а + 1, тогда в силу Аксиом IV.3,1.3 и 1.3 имеем:
• (с = а + 1, 1 > 0)=2> (с + 1 > а + l)=> (с > а).

Далее из а>0 и из а-а~^х= 1 получим: а + а? a~^l > 1 + 0 => => а{ + а"¹) > 1. Если 6 = 1 + а~', то из (1 > 0, а > 0) => b > 0 => Ь~^] >0, тогда a b-b~' > 1 • 6″¹ > 0 => а > b~' М

Утверждение 5.22 говорит о том, что среди положительных чисел нет ни наибольшего, ни наименьшего. Для второй части этого утверждения обобщением является следующая ниже Теорема 5.23.

Теорема 5.23. Упорядоченное поле F всюду плотно, т. е.

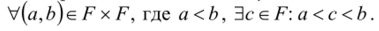
• Пусть 2 = 1 +1 > 0. Поскольку из.

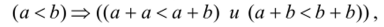
a + b а + b ^~ д а + b ш.

го а < —^— ^и —2— ^< ®' Т^епеР^ь' например, с=- 2 -• ?

Предложения 5.1−5.23 справедливы для любого упорядоченного поля. Но в теории упорядоченного поля F, если F *Q, недоказуемы следующие предложения.

Утверждение 5.24'. Аксиома Архимеда.

Для любых чисел а и Ь, принадлежащих F, 0 <�Ь < а, найдется натуральное число п такое, что, а < b + b + —- + b = b? п .

п слагаемых Утверждение 5.24″. Для каждого положительного а е F найдется

такое натуральное число п, что —<�п.

а Утверждение 5.24″ '. Для всякого as F, а> 0, найдется натуральное число п такое, что < а <2 .

2″ .

Задание 5.1. Приняв одно из Утверждений 5.24 за аксиому поля F, доказать два других.

Упорядоченное поле F, в котором справедливо утверждение 5.24, называется архимедовым полем.

В [30] показано на с. 34−36, что Аксиома VII непрерывности множества R действительных чисел эквивалентна следующим ниже предложениям о полноте множества R.

Предложение VIIПринцип полноты Вейерштрасса. Любое ограниченное сверху непустое множество из R имеет в R точную верхнюю грань.

Предложение VII". Теорема отделимости. Если, А Ф 0 Ф В, AJ В = R

и для У (а, Ь) е Ах В а<�Ь, то в R существует такое с, что для всех (х, у) е Ах В х <�с < у.

Предложение VII". Принцип полноты Кантора множества R.

A. Пусть в R дана система {[a", b_n]}, neN, вложенных отрезков К₊|" б"₊, ] с [й", b_n]czR. Тогда Щ>, Ь,] & 0, т. е. существует число с & R

такое, что Vп eN с е [а" , Ь_п].

B. Архимедово поле F, в котором пересечение системы вложенных отрезков не пусто, есть множество R действительных чисел (ер. [41, с. 76, Теорема 3 и далее]).

Задание 5.2. Доказать справедливость Утверждений 5.24'-5.24″ ' в поле Q рациональных чисел, т. е. что поле Q архимедово.

Вопросы Читателю

• 1. Как можно определить бесконечномерное линейное пространство К*,?
• 2. Как изменится система аксиом множества R. если в качестве одной из них принять Теорему 5.0?
• 3. Можно ли было бы принять числа меньшие нуля за положительные числа? Если «да», то чему бы это противоречило?
• 4. Справедлива ли Теорема отделимости (Предложение VII") во множестве N натуральных чисел? Что из этого следует?
• 5. Каким числом можно заменить в Утверждении 5.24″ ' степень 2″?
• 6. Из и. 2 Главы 7, как Вы увидите, следует существование бесконечно больших натуральных чисел. Противоречит ли это Аксиомам Псано (см. п. 3.7.5, с. 58) множества натуральных чисел?