Простейшие колебательные системы

Простейшими колебательными системами являются маятники. Пружинный маятник (механический осциллятор) представляет собой небольшое тело массой т, соединенное с пружиной жесткостью к (см. рисунок). При смещении его из положения равновесия на величину х возникает возвращающая сила величиной кх, направленная против смещения. Второй закон Ньютона, примененный к этой системе, дает.

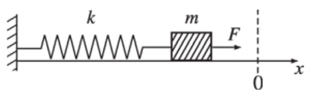
Пружинный маятник.

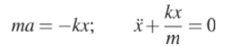
— то же уравнение гармонических колебаний предыдущего раздела, в котором квадрат собственной циклической частоты равен.

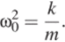
Таким образом, период колебаний пружинного маятника составляет.

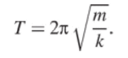
Физический маятник показан на данном рисунке.

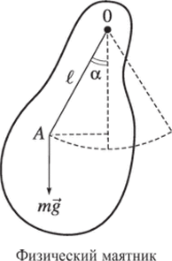
Он представляет собой тело произвольной формы, вращающееся вокруг закрепленной оси 0. В точке А находится центр масс маятника. Возвращающий момент сил М создает сила тяжести. При небольших углах, а отклонения маятника он равен.

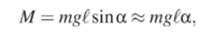
где т — масса маятника, i — расстояние от оси вращения до центра масс маятника. Основное уравнение динамики вращательного движения дает.

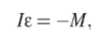
где е = а — угловое ускорение, a / — момент инерции маятника для вышеупомянутой оси. Минус в этой формуле связан с тем, что ускорение положительно тогда, когда угол отрицателен, и наоборот. Уравнение движения физического маятника полностью аналогично предыдущему случаю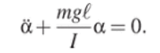

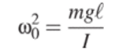
Сравнивая его с общим уравнением свободных гармонических колебаний, заключаем, что маятник совершает гармонические колебания с циклической частотой и периодом.

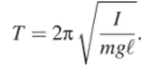
Математический маятник — небольшое тело, подвешенное на нити длины ? — показано на рисунке.

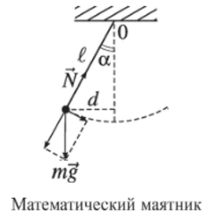
И его уравнение движения сводится к уравнению гармонических колебаний. На маятник действует сила тяжести mg и сила упругости N, показанные на рисунке. Математический маятник является частным случаем физического, причем момент его инерции / = mt². В результате уравнение движения математического маятника принимает вид.

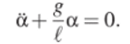
Поэтому период колебаний физического маятника.

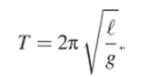
Превращения энергии при гармонических колебаниях.

Гармонические колебания — постоянный процесс перехода кинетической энергии колеблющегося тела в потенциальную и обратно. Например, при максимальном отклонении пружинного маятника вся его энергия сосредоточена в потенциальной энергии деформированной пружины, а для математического и физического маятников — в потенциальной энергии в поле силы тяжести. Скорость и кинетическая энергия в этом положении равны нулю. Наоборот, при прохождении положения равновесия вся энергия маятников кинетическая, скорость максимальна, а потенциальная энергия — нуль. Так как за период тело дважды проходит амплитудные положения и дважды — положение равновесия, каждый вид энергии меняется от нуля до максимума тоже дважды за период. Другими словами, частота колебаний отдельного вида энергии вдвое больше собственной частоты колебаний системы.

Это видно и из формул для энергии. Например, кинетическая энергия колеблющегося тела.

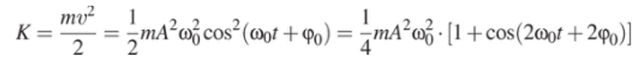
меняется с частотой 2соо. С той же частотой меняется и потенциальная энергия, например, пружинного маятника.

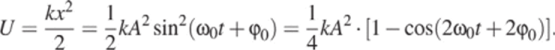
Сложив эти формулы, легко получить величину полной энергии как через максимальную кинетическую, так и через максимальную потенциальную энергию.

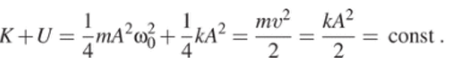
Естественно, что полная энергия от времени не зависит, т. е. сохраняется. Графики К и U показаны на рисунке.

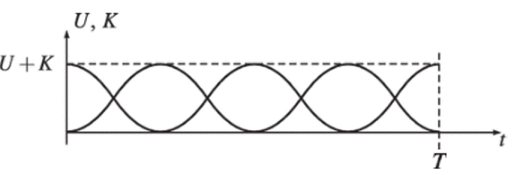
Потенциальная (U) и кинетическая (К) энергии.