Линейные векторные пространства

Определение 2.1. Упорядоченная система из n действительных чисел 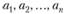называется n-мерным вектором и обозначается 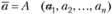. Числа 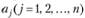называются компонентами вектора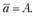

Определение 2.2. Совокупность всевозможных n-мерных векторов с введенными на ней операциями сложения и умножения на число называется n-мерным векторным пространством.

В матрице из т строк и п столбцов строки являются n-мерными векторами, столбцы — m-мерным и векторами.

Вектор 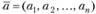и вектор 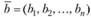равны, если совпадают их компоненты, стоящие на одинаковых местах, т. е. есл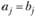и при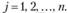

Суммой векторов 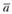и 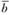называется вектор 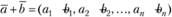. Роль нуля играет нулевой вектор 0 = (0, 0, …, 0).

Противоположным вектору 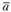называется вектор 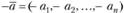; очевидно, что 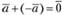. Разность векторов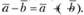

Произведением вектора 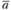на число? называется вектор 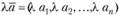. Из этого определения вытекают следующие важные свойства:

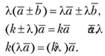
Следствиями этих свойств являются следующие: 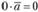, 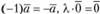. Скалярным произведением двух векторов 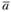и 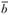(A и В) называется действительное число, равное сумме произведений соответствующих компонент этих векторов:

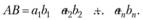
Например, левая часть линейного уравнения 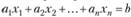может быть представлена в виде скалярного произведения векторов A· Х, где ,.

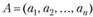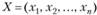
Вектор В называется линейной комбинацией векторов , если существуют такие числа 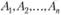, при которых выполняется соотношение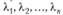

Система векторов 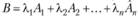называется линейно зависимой, если хотя бы один из векторов системы является линейной комбинацией остальных, и линейно независимой — в противном случае. Можно сформулировать следующие равносильные сказанному определения.

Система векторов 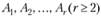- линейно зависимая, если существуют числа 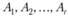, не все равные нулю, при которых имеет место равенство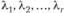

Если последнее соотношение возможно лишь в случае, когда все 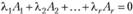, то система векторов называется линейно независимой.

Например, система векторов 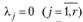, , 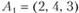линейно зависима: .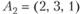

Рангом системы векторов

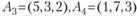
называется максимальное число линейно независимых векторов этой системы. Ранг системы векторов равен рангу матрицы А, составленной из компонент векторов этой системы, т. е. наивысшему порядку минора матрицы А, отличного от нуля.

Пример 2.4. Определить, является ли система векторов , , 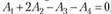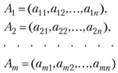линейно зависимой; если она линейно-зависима, то найти ее максимальную линейно независимую подсистему.

Решение. Составим матрицу из компонент векторов и найдем ее ранг.

Имеем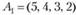

Минор второго порядка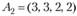

Рассмотрим два минора третьего порядка, которые его окаймляют:

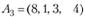
Ранг матрицы А равен 2, поэтому система векторов является зависимой. В матрицах, составленных из компонент любых двух векторов данной системы, содержатся миноры второго порядка, отличные от нуля, например,.

Поэтому максимальная линейно независимая подсистема состоит из двух любых векторов, а третий вектор является их линейной комбинацией.

Базисом n-мерного векторного пространства называется любая совокупность п линейно независимых векторов этого же пространства.

Теорема 2.2. Любой вектор n-мерного векторного пространства можно представить как линейную комбинацию векторов базиса, притом единственным образом.

Один из базисов n-мерного векторного пространства образует система единичных векторов.

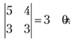
Компоненты любого n-мерного вектора можно считать координатами этого вектора в единичном базисе.

Пусть задано n-мерное линейное пространство

Определение 2.3. Множество X называется выпуклым, если вместе с любыми точками х_{ и х₂ множеству принадлежат точки (отрезок) 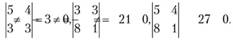при всех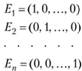

Множество на рис. 2.1, а — выпуклое, на рис. 2.1, б — невыпуклое.

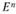
Рис. 2.1

Определение 2.4. Функция 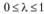, заданная на выпуклом множестве 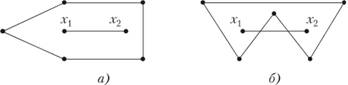, называется выпуклой, если для любых двух точек x₁ и х₂ из X и любого числа 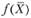выполняется соотношение.

Определение 2.5. Функция 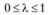, заданная на выпуклом множестве 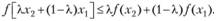, называется вогнутой, если для любых двух точек х₁ и х₂ из X и любого числа 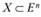выполняется соотношение.

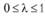
Если приведенные неравенства считать строгими и они выполняются при 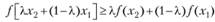, то функция 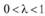- строго выпуклая (вогнутая).

Можно показать, что если 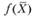- выпуклая функция, то функция 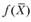- вогнутая, и наоборот.

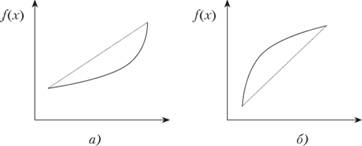
На рис. 2.2, а функция 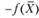- выпуклая, на рис. 2.2, б - вогнутая.

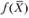
Рис. 2.2

Справедливы следующие утверждения относительно выпуклых множеств и функций.

• 1. Пересечение выпуклых множеств есть выпуклое множество.
• 2. Сумма вогнутых (выпуклых) функций есть вогнутая (выпуклая) функция.
• 3. Если - выпуклая функция при 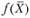, то множество всех точек, удовлетворяющих условиям 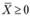, , 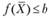выпукло (если оно не пустое; b — это постоянная).
• 4. Пусть 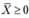- выпуклая (вогнутая) функция, заданная на замкнутом выпуклом множестве 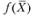, тогда любой локальный минимум (максимум) на X является и глобальным.

Приведем необходимое и достаточное условие выпуклости функции многих переменных. Пусть функция имеет все частные производные второго порядка, образующие матрицу.

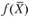
Эта функция является выпуклой в области X тогда и только тогда, когда матрица Q для любой точки из этой области является неотрицательно (положительно) определенной. Напомним, что квадратная матрица 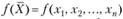называется неотрицательно (положительно) определенной, если все определители.

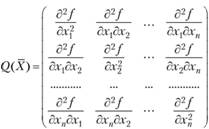
т.е. все главные миноры матрицы, неотрицательны (положительны).

Пример 2.5. Показать, что функция 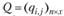является выпуклой при

Составим матрицу из частных производных второго порядка для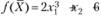

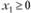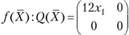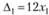Найдем главные миноры . Так как при , то функция является выпуклой.

Дадим определение глобального и локального максимумов. Функция 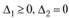достигает на замкнутом (т.е. включающем свою границу) множестве X глобальный максимум в точке 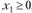, если для любой точки, принадлежащей , выполняется условие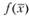

Функция 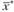достигает на замкнутом множестве X локального максимума в точке 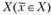, если существует некоторой окрестность этой точки, для каждой точки которой выполняется условие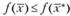

Определения локального и глобального минимума формулируются аналогично.

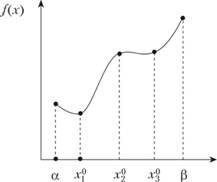
На рис. 2.3 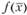- точка локального минимума; 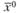- глобального минимума; ?,  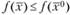— точки локального максимума;? — точка глобального максимума.

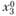
Рис. 2.3

Необходимые условия экстремума (максимума, минимума). Если в точке 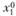функция 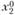имеет экстремум, то частные производные первого порядка равны нулю в этой точке:

Достаточные условия существования экстремума здесь не формулируются. О самом существовании точек глобального минимума и максимума говорит следующая теорема.

Теорема Вейерштрасса

Если функция 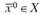определена и непрерывна в ограниченной замкнутой области X, то она достигает в ней своих точных верхней и нижней границ (глобальный максимум и глобальный минимум).

Приведенные утверждения относительно выпуклых множеств и функций, условий существования экстремума позволяют делать выводы о свойствах тех или иных задач оптимального программирования, что является основой разработки и применения математических методов их решения. Например, симплекс-метод решения задачи линейного программирования использует, в частности, «свойство выпуклости» этой задачи: не существует локального экстремума, отличного от глобального.